Analysis
Analysis has always been at the heart of philosophical method, but it has been understood and practised in many different ways. Perhaps, in its broadest sense, it might be defined as a process of isolating or working back to what is more fundamental by means of which something, initially taken as given, can be explained or reconstructed. The explanation or reconstruction is often then exhibited in a corresponding process of synthesis. This allows great variation in specific method, however. The aim may be to get back to basics, but there may be all sorts of ways of doing this, each of which might be called ‘analysis’. The dominance of ‘analytic’ philosophy in the English-speaking world, and increasingly now in the rest of the world, might suggest that a consensus has formed concerning the role and importance of analysis. This assumes, though, that there is agreement on what ‘analysis’ means, and this is far from clear. On the other hand, Wittgenstein's later critique of analysis in the early (logical atomist) period of analytic philosophy, and Quine's attack on the analytic-synthetic distinction, for example, have led some to claim that we are now in a ‘post-analytic’ age. Such criticisms, however, are only directed at particular conceptions of analysis. If we look at the history of philosophy, and even if we just look at the history of analytic philosophy, we find a rich and extensive repertoire of conceptions of analysis which philosophers have continually drawn upon and reconfigured in different ways. Analytic philosophy is alive and well precisely because of the range of conceptions of analysis that it involves. It may have fragmented into various interlocking subtraditions, but those subtraditions are held together by both their shared history and their methodological interconnections. It is the aim of this article to indicate something of the range of conceptions of analysis in the history of philosophy and their interconnections, and to provide a bibliographical resource for those wishing to explore analytic methodologies and the philosophical issues that they raise.
- 1. General Introduction
- 2. Ancient Conceptions of Analysis and the Emergence of the Regressive Conception
- 3. Medieval and Renaissance Conceptions of Analysis
- 4. Early Modern Conceptions of Analysis and the Development of the Decompositional Conception
- 5. Modern Conceptions of Analysis, outside Analytic Philosophy
- 6. Conceptions of Analysis in Analytic Philosophy and the Introduction of the Logical (Transformative) Conception
- 7. Conclusion
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. General Introduction
This section provides a preliminary description of analysis—or the range of different conceptions of analysis—and a guide to this article as a whole.
1.1 Characterizations of Analysis
If asked what ‘analysis’ means, most people today immediately think of breaking something down into its components; and this is how analysis tends to be officially characterized. In the Concise Oxford Dictionary, for example, ‘analysis’ is defined as the “resolution into simpler elements by analysing (opp. synthesis)”, the only other uses mentioned being the mathematical and the psychological [Quotation]. And in the Oxford Dictionary of Philosophy, ‘analysis’ is defined as “the process of breaking a concept down into more simple parts, so that its logical structure is displayed” [Quotation]. The restriction to concepts and the reference to displaying ‘logical structure’ are important qualifications, but the core conception remains that of breaking something down.
This conception may be called the decompositional conception of analysis (see Section 4). But it is not the only conception, and indeed is arguably neither the dominant conception in the pre-modern period nor the conception that is characteristic of at least one major strand in ‘analytic’ philosophy. In ancient Greek thought, ‘analysis’ referred primarily to the process of working back to first principles by means of which something could then be demonstrated. This conception may be called the regressive conception of analysis (see Section 2). In the work of Frege and Russell, on the other hand, before the process of decomposition could take place, the statements to be analyzed had first to be translated into their ‘correct’ logical form (see Section 6). This suggests that analysis also involves a transformative or interpretive dimension. This too, however, has its roots in earlier thought (see especially the supplementary sections on Ancient Greek Geometry and Medieval Philosophy).
These three conceptions should not be seen as competing. In actual practices of analysis, which are invariably richer than the accounts that are offered of them, all three conceptions are typically reflected, though to differing degrees and in differing forms. To analyze something, we may first have to interpret it in some way, translating an initial statement, say, into the privileged language of logic, mathematics or science, before articulating the relevant elements and structures, and all in the service of identifying fundamental principles by means of which to explain it. The complexities that this schematic description suggests can only be appreciated by considering particular types of analysis.
Understanding conceptions of analysis is not simply a matter of attending to the use of the word ‘analysis’ and its cognates—or obvious equivalents in languages other than English, such as ‘analusis’ in Greek or ‘Analyse’ in German. Socratic definition is arguably a form of conceptual analysis, yet the term ‘analusis’ does not occur anywhere in Plato's dialogues (see Section 2 below). Nor, indeed, do we find it in Euclid's Elements, which is the classic text for understanding ancient Greek geometry: Euclid presupposed what came to be known as the method of analysis in presenting his proofs ‘synthetically’. In Latin, ‘resolutio’ was used to render the Greek word ‘analusis’, and although ‘resolution’ has a different range of meanings, it is often used synonymously with ‘analysis’ (see the supplementary section on Renaissance Philosophy). In Aristotelian syllogistic theory, and especially from the time of Descartes, forms of analysis have also involved ‘reduction’; and in early analytic philosophy it was ‘reduction’ that was seen as the goal of philosophical analysis (see especially the supplementary section on The Cambridge School of Analysis).
Further details of characterizations of analysis that have been offered in the history of philosophy, including all the classic passages and remarks (to which occurrences of ‘[Quotation]’ throughout this entry refer), can be found in the supplementary document on
Definitions and Descriptions of Analysis.
A list of key reference works, monographs and collections can be found in the
Annotated Bibliography, §1.
1.2 Guide to this Entry
This entry comprises three sets of documents:
- The present document
- Six supplementary documents (one of which is not yet available)
- An annotated bibliography on analysis, divided into six documents
The present document provides an overview, with introductions to the various conceptions of analysis in the history of philosophy. It also contains links to the supplementary documents, the documents in the bibliography, and other internet resources. The supplementary documents expand on certain topics under each of the six main sections. The annotated bibliography contains a list of key readings on each topic, and is also divided according to the sections of this entry.
2. Ancient Conceptions of Analysis and the Emergence of the Regressive Conception
The word ‘analysis’ derives from the ancient Greek term ‘analusis’. The prefix ‘ana’ means ‘up’, and ‘lusis’ means ‘loosing’, ‘release’ or ‘separation’, so that ‘analusis’ means ‘loosening up’ or ‘dissolution’. The term was readily extended to the solving or dissolving of a problem, and it was in this sense that it was employed in ancient Greek geometry and philosophy. The method of analysis that was developed in ancient Greek geometry had an influence on both Plato and Aristotle. Also important, however, was the influence of Socrates's concern with definition, in which the roots of modern conceptual analysis can be found. What we have in ancient Greek thought, then, is a complex web of methodologies, of which the most important are Socratic definition, which Plato elaborated into his method of division, his related method of hypothesis, which drew on geometrical analysis, and the method(s) that Aristotle developed in his Analytics. Far from a consensus having established itself over the last two millennia, the relationships between these methodologies are the subject of increasing debate today. At the heart of all of them, too, lie the philosophical problems raised by Meno's paradox, which anticipates what we now know as the paradox of analysis, concerning how an analysis can be both correct and informative (see the supplementary section on Moore), and Plato's attempt to solve it through the theory of recollection, which has spawned a vast literature on its own.
‘Analysis’ was first used in a methodological sense in ancient Greek geometry, and the model that Euclidean geometry provided has been an inspiration ever since. Although Euclid's Elements dates from around 300 BC, and hence after both Plato and Aristotle, it is clear that it draws on the work of many previous geometers, most notably, Theaetetus and Eudoxus, who worked closely with Plato and Aristotle. Plato is even credited by Diogenes Laertius (LEP, I, 299) with inventing the method of analysis, but whatever the truth of this may be, the influence of geometry starts to show in his middle dialogues, and he certainly encouraged work on geometry in his Academy.
The classic source for our understanding of ancient Greek geometrical analysis is a passage in Pappus's Mathematical Collection, which was composed around 300 AD, and hence drew on a further six centuries of work in geometry from the time of Euclid's Elements:
Now analysis is the way from what is sought—as if it were admitted—through its concomitants (akolouthôn) in order[,] to something admitted in synthesis. For in analysis we suppose that which is sought to be already done, and we inquire from what it results, and again what is the antecedent of the latter, until we on our backward way light upon something already known and being first in order. And we call such a method analysis, as being a solution backwards (anapalin lysin).In synthesis, on the other hand, we suppose that which was reached last in analysis to be already done, and arranging in their natural order as consequents (epomena) the former antecedents and linking them one with another, we in the end arrive at the construction of the thing sought. And this we call synthesis. [Full Quotation]
Analysis is clearly being understood here in the regressive sense—as involving the working back from ‘what is sought’, taken as assumed, to something more fundamental by means of which it can then be established, through its converse, synthesis. For example, to demonstrate Pythagoras's theorem—that the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides—we may assume as ‘given’ a right-angled triangle with the three squares drawn on its sides. In investigating the properties of this complex figure we may draw further (auxiliary) lines between particular points and find that there are a number of congruent triangles, from which we can begin to work out the relationship between the relevant areas. Pythagoras's theorem thus depends on theorems about congruent triangles, and once these—and other—theorems have been identified (and themselves proved), Pythagoras's theorem can be proved. (The theorem is demonstrated in Proposition 47 of Book I of Euclid's Elements.)
The basic idea here provides the core of the conception of analysis that one can find reflected, in its different ways, in the work of Plato and Aristotle (see the supplementary sections on Plato and Aristotle). Although detailed examination of actual practices of analysis reveals more than just regression to first causes, principles or theorems, but decomposition and transformation as well (see especially the supplementary section on Ancient Greek Geometry), the regressive conception dominated views of analysis until well into the early modern period.
Ancient Greek geometry was not the only source of later conceptions of analysis, however. Plato may not have used the term ‘analysis’ himself, but concern with definition was central to his dialogues, and definitions have often been seen as what ‘conceptual analysis’ should yield. The definition of ‘knowledge’ as ‘justified true belief’ (or ‘true belief with an account’, in more Platonic terms) is perhaps the classic example. Plato's concern may have been with real rather than nominal definitions, with ‘essences’ rather than mental or linguistic contents (see the supplementary section on Plato), but conceptual analysis, too, has frequently been given a ‘realist’ construal. Certainly, the roots of conceptual analysis can be traced back to Plato's search for definitions, as we shall see in Section 4 below.
Further discussion can be found in the supplementary document on
Ancient Conceptions of Analysis.
Further reading can be found in the
Annotated Bibliography, §2.
3. Medieval and Renaissance Conceptions of Analysis
Conceptions of analysis in the medieval and renaissance periods were largely influenced by ancient Greek conceptions. But knowledge of these conceptions was often second-hand, filtered through a variety of commentaries and texts that were not always reliable. Medieval and renaissance methodologies tended to be uneasy mixtures of Platonic, Aristotelian, Stoic, Galenic and neo-Platonic elements, many of them claiming to have some root in the geometrical conception of analysis and synthesis. However, in the late medieval period, clearer and more original forms of analysis started to take shape. In the literature on so-called ‘syncategoremata’ and ‘exponibilia’, for example, we can trace the development of a conception of interpretive analysis. Sentences involving more than one quantifier such as ‘Some donkey every man sees’, for example, were recognized as ambiguous, requiring ‘exposition’ to clarify.
In John Buridan's masterpiece of the mid-fourteenth century, the Summulae de Dialectica, we can find all three of the conceptions outlined in Section 1.1 above. He distinguishes explicitly between divisions, definitions and demonstrations, corresponding to decompositional, interpretive and regressive analysis, respectively. Here, in particular, we have anticipations of modern analytic philosophy as much as reworkings of ancient philosophy. Unfortunately, however, these clearer forms of analysis became overshadowed during the Renaissance, despite—or perhaps because of—the growing interest in the original Greek sources. As far as understanding analytic methodologies was concerned, the humanist repudiation of scholastic logic muddied the waters.
Further discussion can be found in the supplementary document on
Medieval and Renaissance Conceptions of Analysis.
Further reading can be found in the
Annotated Bibliography, §3.
4. Early Modern Conceptions of Analysis and the Development of the Decompositional Conception
The scientific revolution in the seventeenth century brought with it new forms of analysis. The newest of these emerged through the development of more sophisticated mathematical techniques, but even these still had their roots in earlier conceptions of analysis. By the end of the early modern period, decompositional analysis had become dominant (as outlined in what follows), but this, too, took different forms, and the relationships between the various conceptions of analysis were often far from clear.
In common with the Renaissance, the early modern period was marked by a great concern with methodology. This might seem unsurprising in such a revolutionary period, when new techniques for understanding the world were being developed and that understanding itself was being transformed. But what characterizes many of the treatises and remarks on methodology that appeared in the seventeenth century is their appeal, frequently self-conscious, to ancient methods (despite, or perhaps—for diplomatic reasons—because of, the critique of the content of traditional thought), although new wine was generally poured into the old bottles. The model of geometrical analysis was a particular inspiration here, albeit filtered through the Aristotelian tradition, which had assimilated the regressive process of going from theorems to axioms with that of moving from effects to causes (see the supplementary section on Aristotle). Analysis came to be seen as a method of discovery, working back from what is ordinarily known to the underlying reasons (demonstrating ‘the fact’), and synthesis as a method of proof, working forwards again from what is discovered to what needed explanation (demonstrating ‘the reason why’). Analysis and synthesis were thus taken as complementary, although there remained disagreement over their respective merits.
There is a manuscript by Galileo, dating from around 1589, an appropriated commentary on Aristotle's Posterior Analytics, which shows his concern with methodology, and regressive analysis, in particular (see Wallace 1992a and 1992b). Hobbes wrote a chapter on method in the first part of De Corpore, published in 1655, which offers his own interpretation of the method of analysis and synthesis, where decompositional forms of analysis are articulated alongside regressive forms [Quotations]. But perhaps the most influential account of methodology, from the middle of the seventeenth century until well into the nineteenth century, was the fourth part of the Port-Royal Logic, the first edition of which appeared in 1662 and the final revised edition in 1683. Chapter 2 (which was the first chapter in the first edition) opens as follows:
The art of arranging a series of thoughts properly, either for discovering the truth when we do not know it, or for proving to others what we already know, can generally be called method.Hence there are two kinds of method, one for discovering the truth, which is known as analysis, or the method of resolution, and which can also be called the method of discovery. The other is for making the truth understood by others once it is found. This is known as synthesis, or the method of composition, and can also be called the method of instruction. [Fuller Quotations]
That a number of different methods might be assimilated here is not noted, although the text does go on to distinguish four main types of ‘issues concerning things’: seeking causes by their effects, seeking effects by their causes, finding the whole from the parts, and looking for another part from the whole and a given part (ibid., 234). While the first two involve regressive analysis and synthesis, the third and fourth involve decompositional analysis and synthesis.
As the authors of the Logic make clear, this particular part of their text derives from Descartes's Rules for the Direction of the Mind, written around 1627, but only published posthumously in 1684. The specification of the four types was most likely offered in elaborating Descartes's Rule Thirteen, which states: “If we perfectly understand a problem we must abstract it from every superfluous conception, reduce it to its simplest terms and, by means of an enumeration, divide it up into the smallest possible parts.” (PW, I, 51. Cf. the editorial comments in PW, I, 54, 77.) The decompositional conception of analysis is explicit here, and if we follow this up into the later Discourse on Method, published in 1637, the focus has clearly shifted from the regressive to the decompositional conception of analysis. All the rules offered in the earlier work have now been reduced to just four. This is how Descartes reports the rules he says he adopted in his scientific and philosophical work:
The first was never to accept anything as true if I did not have evident knowledge of its truth: that is, carefully to avoid precipitate conclusions and preconceptions, and to include nothing more in my judgements than what presented itself to my mind so clearly and so distinctly that I had no occasion to doubt it.The second, to divide each of the difficulties I examined into as many parts as possible and as may be required in order to resolve them better.
The third, to direct my thoughts in an orderly manner, by beginning with the simplest and most easily known objects in the order to ascend little by little, step by step, to knowledge of the most complex, and by supposing some order even among objects that have no natural order of precedence.
And the last, throughout to make enumerations so complete, and reviews so comprehensive, that I could be sure of leaving nothing out. (PW, I, 120.)
The first two are rules of analysis and the second two rules of synthesis. But although the analysis/synthesis structure remains, what is involved here is decomposition/composition rather than regression/progression. Nevertheless, Descartes insisted that it was geometry that influenced him here: “Those long chains composed of very simple and easy reasonings, which geometers customarily use to arrive at their most difficult demonstrations, had given me occasion to suppose that all the things which can fall under human knowledge are interconnected in the same way.” (Ibid. [Further Quotations])
Descartes's geometry did indeed involve the breaking down of complex problems into simpler ones. More significant, however, was his use of algebra in developing ‘analytic’ geometry as it came to be called, which allowed geometrical problems to be transformed into arithmetical ones and more easily solved. In representing the ‘unknown’ to be found by ‘x’, we can see the central role played in analysis by the idea of taking something as ‘given’ and working back from that, which made it seem appropriate to regard algebra as an ‘art of analysis’, alluding to the regressive conception of the ancients. Illustrated in analytic geometry in its developed form, then, we can see all three of the conceptions of analysis outlined in Section 1.1 above, despite Descartes's own emphasis on the decompositional conception. For further discussion of this, see the supplementary section on Descartes and Analytic Geometry.
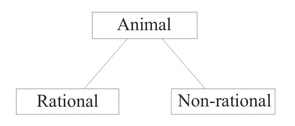
Descartes's emphasis on decompositional analysis was not without precedents, however. Not only was it already involved in ancient Greek geometry, but it was also implicit in Plato's method of collection and division. We might explain the shift from regressive to decompositional (conceptual) analysis, as well as the connection between the two, in the following way. Consider a simple example, as represented in the diagram below, ‘collecting’ all animals and ‘dividing’ them into rational and non-rational, in order to define human beings as rational animals.
On this model, in seeking to define anything, we work back up the appropriate classificatory hierarchy to find the higher (i.e., more basic or more general) ‘Forms’, by means of which we can lay down the definition. Although Plato did not himself use the term ‘analysis’—the word for ‘division’ was ‘dihairesis’—the finding of the appropriate ‘Forms’ is essentially analysis. As an elaboration of the Socratic search for definitions, we clearly have in this the origins of conceptual analysis. There is little disagreement that ‘Human beings are rational animals’ is the kind of definition we are seeking, defining one concept, the concept human being, in terms of other concepts, the concepts rational and animal. But the construals that have been offered of this have been more problematic. Understanding a classificatory hierarchy extensionally, that is, in terms of the classes of things denoted, the classes higher up are clearly the larger, ‘containing’ the classes lower down as subclasses (e.g., the class of animals includes the class of human beings as one of its subclasses). Intensionally, however, the relationship of ‘containment’ has been seen as holding in the opposite direction. If someone understands the concept human being, at least in the strong sense of knowing its definition, then they must understand the concepts animal and rational; and it has often then seemed natural to talk of the concept human being as ‘containing’ the concepts rational and animal. Working back up the hierarchy in ‘analysis’ (in the regressive sense) could then come to be identified with ‘unpacking’ or ‘decomposing’ a concept into its ‘constituent’ concepts (‘analysis’ in the decompositional sense). Of course, talking of ‘decomposing’ a concept into its ‘constituents’ is, strictly speaking, only a metaphor (as Quine was famously to remark in §1 of ‘Two Dogmas of Empiricism’), but in the early modern period, this began to be taken more literally.
For further discussion, see the supplementary document on
Early Modern Conceptions of Analysis,
which contains sections on Descartes and Analytic Geometry, British Empiricism, Leibniz, and Kant.
For further reading, see the
Annotated Bibliography, §4.
5. Modern Conceptions of Analysis, outside Analytic Philosophy
As suggested in the supplementary document on Kant, the decompositional conception of analysis found its classic statement in the work of Kant at the end of the eighteenth century. But Kant was only expressing a conception widespread at the time. The conception can be found in a very blatant form, for example, in the writings of Moses Mendelssohn, for whom, unlike Kant, it was applicable even in the case of geometry [Quotation]. Typified in Kant's and Mendelssohn's view of concepts, it was also reflected in scientific practice. Indeed, its popularity was fostered by the chemical revolution inaugurated by Lavoisier in the late eighteenth century, the comparison between philosophical analysis and chemical analysis being frequently drawn. As Lichtenberg put it, “Whichever way you look at it, philosophy is always analytical chemistry” [Quotation].
This decompositional conception of analysis set the methodological agenda for philosophical approaches and debates in the (late) modern period (nineteenth and twentieth centuries). Responses and developments, very broadly, can be divided into two. On the one hand, an essentially decompositional conception of analysis was accepted, but a critical attitude was adopted towards it. If analysis simply involved breaking something down, then it appeared destructive and life-diminishing, and the critique of analysis that this view engendered was a common theme in idealism and romanticism in all its main varieties—from German, British and French to North American. One finds it reflected, for example, in remarks about the negating and soul-destroying power of analytical thinking by Schiller [Quotation], Hegel [Quotation] and de Chardin [Quotation], in Bradley's doctrine that analysis is falsification [Quotation], and in the emphasis placed by Bergson on ‘intuition’ [Quotation].
On the other hand, analysis was seen more positively, but the Kantian conception underwent a certain degree of modification and development. In the nineteenth century, this was exemplified, in particular, by Bolzano and the neo-Kantians. Bolzano's most important innovation was the method of variation, which involves considering what happens to the truth-value of a sentence when a constituent term is substituted by another. This formed the basis for his reconstruction of the analytic/synthetic distinction, Kant's account of which he found defective. The neo-Kantians emphasized the role of structure in conceptualized experience and had a greater appreciation of forms of analysis in mathematics and science. In many ways, their work attempts to do justice to philosophical and scientific practice while recognizing the central idealist claim that analysis is a kind of abstraction that inevitably involves falsification or distortion. On the neo-Kantian view, the complexity of experience is a complexity of form and content rather than of separable constituents, requiring analysis into ‘moments’ or ‘aspects’ rather than ‘elements’ or ‘parts’. In the 1910s, the idea was articulated with great subtlety by Ernst Cassirer [Quotation], and became familiar in Gestalt psychology.
In the twentieth century, both analytic philosophy and phenomenology can be seen as developing far more sophisticated conceptions of analysis, which draw on but go beyond mere decompositional analysis. The following Section offers an account of analysis in analytic philosophy, illustrating the range and richness of the conceptions and practices that arose. But it is important to see these in the wider context of twentieth-century methodological practices and debates, for it is not just in ‘analytic’ philosophy—despite its name—that analytic methods are accorded a central role. Phenomenology, in particular, contains its own distinctive set of analytic methods, with similarities and differences to those of analytic philosophy. Phenomenological analysis has frequently been compared to conceptual clarification in the ordinary language tradition, for example, and the method of ‘phenomenological reduction’ that Husserl invented in 1905 offers a striking parallel to the reductive project opened up by Russell's theory of descriptions, which also made its appearance in 1905.
Just like Frege and Russell, Husserl's initial concern was with the foundations of mathematics, and in this shared concern we can see the continued influence of the regressive conception of analysis. According to Husserl, the aim of ‘eidetic reduction’, as he called it, was to isolate the ‘essences’ that underlie our various forms of thinking, and to apprehend them by ‘essential intuition’ (‘Wesenserschauung’). The terminology may be different, but this resembles Russell's early project to identify the ‘indefinables’ of philosophical logic, as he described it, and to apprehend them by ‘acquaintance’ (cf. POM, xx). Furthermore, in Husserl's later discussion of ‘explication’ (cf. EJ, §§ 22-4 [Quotations]), we find appreciation of the ‘transformative’ dimension of analysis, which can be fruitfully compared with Carnap's account of explication (see the supplementary section on Carnap and Logical Positivism). Carnap himself describes Husserl's idea here as one of “the synthesis of identification between a confused, nonarticulated sense and a subsequently intended distinct, articulated sense” (1950, 3 [Quotation]).
Phenomenology is not the only source of analytic methodologies outside those of the analytic tradition. Mention might be made here, too, of R. G. Collingwood, working within the tradition of British idealism, which was still a powerful force prior to the Second World War. In his Essay on Philosophical Method (1933), for example, he criticizes Moorean philosophy, and develops his own response to what is essentially the paradox of analysis (concerning how an analysis can be both correct and informative), which he recognizes as having its root in Meno's paradox. In his Essay on Metaphysics (1940), he puts forward his own conception of metaphysical analysis, in direct response to what he perceived as the mistaken repudiation of metaphysics by the logical positivists. Metaphysical analysis is characterized here as the detection of ‘absolute presuppositions’, which are taken as underlying and shaping the various conceptual practices that can be identified in the history of philosophy and science. Even among those explicitly critical of central strands in analytic philosophy, then, analysis in one form or another can still be seen as alive and well.
For further reading, see the
Annotated Bibliography, §5.
6. Conceptions of Analysis in Analytic Philosophy and the Introduction of the Logical (Transformative) Conception
If anything characterizes ‘analytic’ philosophy, then it is presumably the emphasis placed on analysis. But as the foregoing sections have shown, there is a wide range of conceptions of analysis, so such a characterization says nothing that would distinguish analytic philosophy from much of what has either preceded or developed alongside it. Given that the decompositional conception is usually offered as the main conception today, it might be thought that it is this that characterizes analytic philosophy. But this conception was prevalent in the early modern period, shared by both the British Empiricists and Leibniz, for example. Given that Kant denied the importance of decompositional analysis, however, it might be suggested that what characterizes analytic philosophy is the value it places on such analysis. This might be true of Moore's early work, and of one strand within analytic philosophy; but it is not generally true. What characterizes analytic philosophy as it was founded by Frege and Russell is the role played by logical analysis, which depended on the development of modern logic. Although other and subsequent forms of analysis, such as linguistic analysis, were less wedded to systems of formal logic, the central insight motivating logical analysis remained.
Pappus's account of method in ancient Greek geometry suggests that the regressive conception of analysis was dominant at the time—however much other conceptions may also have been implicitly involved (see the supplementary section on Ancient Greek Geometry). In the early modern period, the decompositional conception became widespread (see Section 4). What characterizes analytic philosophy—or at least that central strand that originates in the work of Frege and Russell—is the recognition of what was called earlier the transformative or interpretive dimension of analysis (see Section 1.1). Any analysis presupposes a particular framework of interpretation, and work is done in interpreting what we are seeking to analyze as part of the process of regression and decomposition. This may involve transforming it in some way, in order for the resources of a given theory or conceptual framework to be brought to bear. Euclidean geometry provides a good illustration of this. But it is even more obvious in the case of analytic geometry, where the geometrical problem is first ‘translated’ into the language of algebra and arithmetic in order to solve it more easily (see the supplementary section on Descartes and Analytic Geometry). What Descartes and Fermat did for analytic geometry, Frege and Russell did for analytic philosophy. Analytic philosophy is ‘analytic’ much more in the sense that analytic geometry is ‘analytic’ than in the crude decompositional sense that Kant understood it.
The interpretive dimension of modern philosophical analysis can also be seen as anticipated in medieval scholasticism (see the supplementary section on Medieval Philosophy), and it is remarkable just how much of modern concerns with propositions, meaning, reference, and so on, can be found in the medieval literature. Interpretive analysis is also illustrated in the nineteenth century by Bentham's conception of paraphrasis, which he characterized as “that sort of exposition which may be afforded by transmuting into a proposition, having for its subject some real entity, a proposition which has not for its subject any other than a fictitious entity” [Full Quotation]. He applied the idea in ‘analyzing away’ talk of ‘obligations’, and the anticipation that we can see here of Russell's theory of descriptions has been noted by, among others, Wisdom (1931) and Quine in ‘Five Milestones of Empiricism’ [Quotation].
What was crucial in the emergence of twentieth-century analytic philosophy, however, was the development of quantificational theory, which provided a far more powerful interpretive system than anything that had hitherto been available. In the case of Frege and Russell, the system into which statements were ‘translated’ was predicate logic, and the divergence that was thereby opened up between grammatical and logical form meant that the process of translation itself became an issue of philosophical concern. This induced greater self-consciousness about our use of language and its potential to mislead us, and inevitably raised semantic, epistemological and metaphysical questions about the relationships between language, logic, thought and reality which have been at the core of analytic philosophy ever since.
Both Frege and Russell (after the latter's initial flirtation with idealism) were concerned to show, against Kant, that arithmetic is a system of analytic and not synthetic truths. In the Grundlagen, Frege had offered a revised conception of analyticity, which arguably endorses and generalizes Kant's logical as opposed to phenomenological criterion, i.e., (ANL) rather than (ANO) (see the supplementary section on Kant):
(AN) A truth is analytic if its proof depends only on general logical laws and definitions.
The question of whether arithmetical truths are analytic then comes down to the question of whether they can be derived purely logically. (Here we already have ‘transformation’, at the theoretical level—involving a reinterpretation of the concept of analyticity.) To demonstrate this, Frege realized that he needed to develop logical theory in order to formalize mathematical statements, which typically involve multiple generality (e.g., ‘Every natural number has a successor’, i.e. ‘For every natural number x there is another natural number y that is the successor of x’). This development, by extending the use of function-argument analysis in mathematics to logic and providing a notation for quantification, was essentially the achievement of his first book, the Begriffsschrift (1879), where he not only created the first system of predicate logic but also, using it, succeeded in giving a logical analysis of mathematical induction (see Frege FR, 47-78).
In his second book, Die Grundlagen der Arithmetik (1884), Frege went on to provide a logical analysis of number statements. His central idea was that a number statement contains an assertion about a concept. A statement such as ‘Jupiter has four moons’ is to be understood not as predicating of Jupiter the property of having four moons, but as predicating of the concept moon of Jupiter the second-level property has four instances, which can be logically defined. The significance of this construal can be brought out by considering negative existential statements (which are equivalent to number statements involving the number 0). Take the following negative existential statement:
(0a) Unicorns do not exist.
If we attempt to analyze this decompositionally, taking its grammatical form to mirror its logical form, then we find ourselves asking what these unicorns are that have the property of non-existence. We may then be forced to posit the subsistence—as opposed to existence—of unicorns, just as Meinong and the early Russell did, in order for there to be something that is the subject of our statement. On the Fregean account, however, to deny that something exists is to say that the relevant concept has no instances: there is no need to posit any mysterious object. The Fregean analysis of (0a) consists in rephrasing it into (0b), which can then be readily formalized in the new logic as (0c):
(0b) The concept unicorn is not instantiated.(0c) ~(∃x) Fx.
Similarly, to say that God exists is to say that the concept God is (uniquely) instantiated, i.e., to deny that the concept has 0 instances (or 2 or more instances). On this view, existence is no longer seen as a (first-level) predicate, but instead, existential statements are analyzed in terms of the (second-level) predicate is instantiated, represented by means of the existential quantifier. As Frege notes, this offers a neat diagnosis of what is wrong with the ontological argument, at least in its traditional form (GL, §53). All the problems that arise if we try to apply decompositional analysis (at least straight off) simply drop away, although an account is still needed, of course, of concepts and quantifiers.
The possibilities that this strategy of ‘translating’ into a logical language opens up are enormous: we are no longer forced to treat the surface grammatical form of a statement as a guide to its ‘real’ form, and are provided with a means of representing that form. This is the value of logical analysis: it allows us to ‘analyze away’ problematic linguistic expressions and explain what it is ‘really’ going on. This strategy was employed, most famously, in Russell's theory of descriptions, which was a major motivation behind the ideas of Wittgenstein's Tractatus (see the supplementary sections on Russell and Wittgenstein). Although subsequent philosophers were to question the assumption that there could ever be a definitive logical analysis of a given statement, the idea that ordinary language may be systematically misleading has remained.
To illustrate this, consider the following examples from Ryle's classic 1932 paper, ‘Systematically Misleading Expressions’:
(Ua) Unpunctuality is reprehensible.(Ta) Jones hates the thought of going to hospital.
In each case, we might be tempted to make unnecessary reifications, taking ‘unpunctuality’ and ‘the thought of going to hospital’ as referring to objects. It is because of this that Ryle describes such expressions as ‘systematically misleading’. (Ua) and (Ta) must therefore be rephrased:
(Ub) Whoever is unpunctual deserves that other people should reprove him for being unpunctual.(Tb) Jones feels distressed when he thinks of what he will undergo if he goes to hospital.
In these formulations, there is no overt talk at all of ‘unpunctuality’ or ‘thoughts’, and hence nothing to tempt us to posit the existence of any corresponding entities. The problems that otherwise arise have thus been ‘analyzed away’.
At the time that Ryle wrote ‘Systematically Misleading Expressions’, he, too, assumed that every statement had an underlying logical form that was to be exhibited in its ‘correct’ formulation [Quotations]. But when he gave up this assumption (for reasons indicated in the supplementary section on The Cambridge School of Analysis), he did not give up the motivating idea of logical analysis—to show what is wrong with misleading expressions. In The Concept of Mind (1949), for example, he sought to explain what he called the ‘category-mistake’ involved in talk of the mind as a kind of ‘Ghost in the Machine’. His aim, he wrote, was to “rectify the logical geography of the knowledge which we already possess” (1949, 9), an idea that was to lead to the articulation of connective rather than reductive conceptions of analysis, the emphasis being placed on elucidating the relationships between concepts without assuming that there is a privileged set of intrinsically basic concepts (see the supplementary section on Oxford Linguistic Philosophy).
What these various forms of logical analysis suggest, then, is that what characterizes analysis in analytic philosophy is something far richer than the mere ‘decomposition’ of a concept into its ‘constituents’. But this is not to say that the decompositional conception of analysis plays no role at all. It can be found in the early work of Moore, for example (see the supplementary section on Moore). It might also be seen as reflected in the approach to the analysis of concepts that seeks to specify the necessary and sufficient conditions for their correct employment. Conceptual analysis in this sense goes back to the Socrates of Plato's early dialogues (see the supplementary section on Plato). But it arguably reached its heyday in the 1950s and 1960s. As mentioned in Section 2 above, the definition of ‘knowledge’ as ‘justified true belief’ is perhaps the most famous example; and this definition was criticised in Gettier's classic paper of 1963. (For details of this, see the entry in this Encyclopedia on The Analysis of Knowledge.) The specification of necessary and sufficient conditions may no longer be seen as the primary aim of conceptual analysis, especially in the case of philosophical concepts such as ‘knowledge’, which are fiercely contested; but consideration of such conditions remains a useful tool in the analytic philosopher's toolbag.
For a more detailed account of the these and related conceptions of analysis, see the supplementary document on
Conceptions of Analysis in Analytic Philosophy.
For further reading, see the
Annotated Bibliography, §6.
7. Conclusion
The history of philosophy reveals a rich source of conceptions of analysis. Their origin may lie in ancient Greek geometry, and to this extent the history of analytic methodologies might be seen as a series of footnotes to Euclid. But analysis developed in different though related ways in the two traditions stemming from Plato and Aristotle, the former based on the search for definitions and the latter on the idea of regression to first causes. The two poles represented in these traditions defined methodological space until well into the early modern period, and in some sense is still reflected today. The creation of analytic geometry in the seventeenth century introduced a more reductive form of analysis, and an analogous and even more powerful form was introduced around the turn of the twentieth century in the logical work of Frege and Russell. Although conceptual analysis, construed decompositionally from the time of Leibniz and Kant, and mediated by the work of Moore, is often viewed as characteristic of analytic philosophy, logical analysis, taken as involving translation into a logical system, is what inaugurated the analytic tradition. Analysis has also frequently been seen as reductive, but connective forms of analysis are no less important. Connective analysis, historically inflected, would seem to be particularly appropriate, for example, in understanding analysis itself.
Bibliography
What follows here is a selection of thirty classic and recent works published over the last half-century that together cover the range of different conceptions of analysis in the history of philosophy. A fuller bibliography, which includes all references cited, is provided as a set of supplementary documents, divided to correspond to the sections of this entry:
Annotated Bibliography on Analysis
- Baker, Gordon, 2004, Wittgenstein's Method, Oxford: Blackwell, especially essays 1, 3, 4, 10, 12
- Baldwin, Thomas, 1990, G.E. Moore, London: Routledge, ch. 7
- Beaney, Michael, 2004, ‘Carnap's Conception of Explication: From Frege to Husserl?’, in S. Awodey and C. Klein, (eds.), Carnap Brought Home: The View from Jena, Chicago: Open Court, pp. 117-50
- –––, 2005, ‘Collingwood's Conception of Presuppositional Analysis’, Collingwood and British Idealism Studies 11, no. 2, 41-114
- –––, (ed.), 2007, The Analytic Turn: Analysis in Early Analytic Philosophy and Phenomenology, London: Routledge [includes papers on Frege, Russell, Wittgenstein, C.I. Lewis, Bolzano, Husserl]
- Byrne, Patrick H., 1997, Analysis and Science in Aristotle, Albany: State University of New York Press
- Cohen, L. Jonathan, 1986, The Dialogue of Reason: An Analysis of Analytical Philosophy, Oxford: Oxford University Press, chs. 1-2
- Dummett, Michael, 1991, Frege: Philosophy of Mathematics, London: Duckworth, chs. 3-4, 9-16
- Engfer, Hans-Jürgen, 1982, Philosophie als Analysis, Stuttgart-Bad Cannstatt: Frommann-Holzboog [Descartes, Leibniz, Wolff, Kant]
- Garrett, Aaron V., 2003, Meaning in Spinoza's Method, Cambridge: Cambridge University Press, ch. 4
- Gaukroger, Stephen, 1989, Cartesian Logic, Oxford: Oxford University Press, ch. 3
- Gentzler, Jyl, (ed.), 1998, Method in Ancient Philosophy, Oxford: Oxford University Press [includes papers on Socrates, Plato, Aristotle, mathematics and medicine]
- Gilbert, Neal W., 1960, Renaissance Concepts of Method, New York: Columbia University Press
- Hacker, P.M.S., 1996, Wittgenstein's Place in Twentieth-Century Analytic Philosophy, Oxford: Blackwell
- Hintikka, Jaakko and Remes, Unto, 1974, The Method of Analysis, Dordrecht: D. Reidel [ancient Greek geometrical analysis]
- Hylton, Peter, 2005, Propositions, Functions, Analysis: Selected Essays on Russell's Philosophy, Oxford: Oxford University Press
- –––, 2007, Quine, London: Routledge, ch. 9
- Jackson, Frank, 1998, From Metaphysics to Ethics: A Defence of Conceptual Analysis, Oxford: Oxford University Press, chs. 2-3
- Kretzmann, Norman, 1982, ‘Syncategoremata, exponibilia, sophistimata’, in N. Kretzmann et al., (eds.), The Cambridge History of Later Medieval Philosophy, Cambridge: Cambridge University Press, 211-45
- Menn, Stephen, 2002, ‘Plato and the Method of Analysis’, Phronesis 47, 193-223
- Otte, Michael and Panza, Marco, (eds.), 1997, Analysis and Synthesis in Mathematics, Dordrecht: Kluwer
- Rorty, Richard, (ed.), 1967, The Linguistic Turn, Chicago: University of Chicago Press [includes papers on analytic methodology]
- Rosen, Stanley, 1980, The Limits of Analysis, New York: Basic Books, repr. Indiana: St. Augustine's Press, 2000 [critique of analytic philosophy from a ‘continental’ perspective]
- Sayre, Kenneth M., 1969, Plato's Analytic Method, Chicago: University of Chicago Press
- –––, 2006, Metaphysics and Method in Plato's Statesman, Cambridge: Cambridge University Press, Part I
- Soames, Scott, 2003, Philosophical Analysis in the Twentieth Century, Volume 1: The Dawn of Analysis, Volume 2: The Age of Meaning, New Jersey: Princeton University Press [includes chapters on Moore, Russell, Wittgenstein, logical positivism, Quine, ordinary language philosophy, Davidson, Kripke]
- Strawson, P.F., 1992, Analysis and Metaphysics: An Introduction to Philosophy, Oxford: Oxford University Press, chs. 1-2
- Sweeney, Eileen C., 1994, ‘Three Notions of Resolutio and the Structure of Reasoning in Aquinas’, The Thomist 58, 197-243
- Timmermans, Benoît, 1995, La résolution des problèmes de Descartes à Kant, Paris: Presses Universitaires de France
- Urmson, J.O., 1956, Philosophical Analysis: Its Development between the Two World Wars, Oxford: Oxford University Press
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
- Analysis, a journal in philosophy.
- Bertrand Russell Archives
Acknowledgments
In first composing this entry (in 2002-3) and then revising the main entry and bibliography (in 2007), I have drawn on a number of my published writings (especially Beaney 1996, 2000, 2002, 2007b, 2007c; see Annotated Bibliography §6.1, §6.2). I am grateful to the respective publishers for permission to use this material. Research on conceptions of analysis in the history of philosophy was initially undertaken while a Research Fellow at the Institut für Philosophie of the University of Erlangen-Nürnberg during 1999-2000, and further work was carried out while a Research Fellow at the Institut für Philosophie of the University of Jena during 2006-7, in both cases funded by the Alexander von Humboldt-Stiftung. In the former case, the account was written up while at the Open University (UK), and in the latter case, I had additional research leave from the University of York. I acknowledge the generous support given to me by all five institutions. I am also grateful to the editors of this Encyclopedia, and to Gideon Rosen and Edward N. Zalta, in particular, for comments and suggestions on the content and organisation of this entry in both its initial and revised form. I would like to thank John Ongley, too, for reviewing the first version of this entry, which has helped me to improve it (see Annotated Bibliography §1.3). In updating the bibliography (in 2007), I am indebted to various people who have notified me of relevant works, and especially, Gyula Klima (regarding §2.1), Anna-Sophie Heinemann (regarding §§ 4.2 and 4.4), and Jan Wolenski (regarding §5.3). I invite anyone who has further suggestions of items to be included or comments on the article itself to email me at the address given below.