Imre Lakatos
Imre Lakatos (1922–1974) was a Hungarian-born philosopher of mathematics and science who rose to prominence in Britain, having fled his native land in 1956 when the Hungarian Uprising was suppressed by Soviet tanks. He was notable for his anti-formalist philosophy of mathematics (where “formalism” is not just the philosophy of Hilbert and his followers but also comprises logicism and intuitionism) and for his “Methodology of Scientific Research Programmes” or MSRP, a radical revision of Popper’s Demarcation Criterion between science and non-science which gave rise to a novel theory of scientific rationality.
Although he lived and worked in London, rising to the post of Professor of Logic at the London School of Economics (LSE), Lakatos never became a British citizen, but died a stateless person. Despite the star-studded array of academic lords and knights who were willing to testify on his behalf, neither MI5 nor the Special Branch seem to have trusted him, and no less a person than Roy Jenkins, the then Home Secretary, signed off on the refusal to naturalize him. (See Bandy 2009: ch. 16, which includes the transcripts of successive interrogations.)
Nonetheless, Lakatos’s influence, particularly in the philosophy of science, has been immense. According to Google Scholar, by the 25th of January 2015, that is, just twenty-five days into the new year, thirty-three papers had been published citing Lakatos in that year alone, a citation rate of over one paper per day. Introductory texts on the Philosophy of Science typically include substantial sections on Lakatos, some admiring, some critical, and many an admixture of the two (see for example Chalmers 2013 and Godfrey-Smith 2003). The premier prize for the best book in the Philosophy of Science (funded by the foundation of a wealthy and academically distinguished disciple, Spiro Latsis) is named in his honour. Moreover, Lakatos is one of those philosophers whose influence extends well beyond the confines of academic philosophy. Of the thirty-three papers citing Lakatos published in the first twenty-five days of 2015, at most ten qualify as straight philosophy. The rest are devoted to such topics as educational theory, international relations, public policy research (with special reference to the development of technology), informatics, design science, religious studies, clinical psychology, social economics, political economy, mathematics, the history of physics and the sociology of the family. Thus Imre Lakatos was very much more than a philosophers’ philosopher.
First, we discuss Lakatos’s life in relation to his works. Lakatos’s Hungarian career has now become a big issue in the critical literature. This is partly because of disturbing facts about Lakatos’s early life that have only come to light in the West since his death, and partly because of a dispute between the “Hungarian” and the “English” interpreters of Lakatos’s thought, between those writers (not all of them Magyars) who take the later Lakatos to be much more of a Hegelian (and perhaps much more of a disciple of György Lukács) than he liked to let on, and those who take his Hegelianism to be an increasingly residual affair, not much more, in the end, than a habit of “coquetting” with Hegelian expressions (Marx, Capital: 103). Just as there are analytic Marxists who think that Marx’s thought can be rationally reconstructed without the Hegelian coquetry and dialectical Marxists who think that it cannot, so also there are analytic Lakatosians who think that Lakatos’s thought can be largely reconstructed without the Hegelian coquetry and dialectical Lakatosians who think that it cannot (see for instance Kadvany 2001 and Larvor 1998). Obviously, we cannot settle the matter in an Encyclopedia entry but we hope to say enough to illuminate the issue. (Spoiler alert: so far as the Philosophy of Science is concerned, we tend to favor the English interpretation. We are more ambivalent with respect to the Philosophy of Mathematics.)
Secondly we discuss Lakatos’s big ideas, the two contributions that constitute his chief claims to fame as a philosopher, before moving on (thirdly) to a more detailed discussion of some of his principal papers. We conclude with a section on the Feyerabend/Lakatos Debate. Lakatos was a provocative and combative thinker, and it falsifies his thought to present it as less controversial (and perhaps less outrageous) than it actually was.
Note: In referring to Lakatos’s chief works (and to a couple of Popper’s) we have employed a set of acronyms rather than the name/date system, hoping that this will be more perspicuous to readers. The acronyms are explained in the Bibliography.
- 1. Life
- 2. Lakatos’s Big Ideas
- 3. Works
- 3.1 Proofs and Refutations (1963–4, 1976)
- 3.2 “Regress” and “Renaissance”
- 3.3 “Changes in the Problem of Inductive Logic” (1968)
- 3.4 “Falsification and the Methodology of Scientific Research Programmes” (1970)
- 3.5 “The History of Science and Its Rational Reconstructions” (1971)
- 3.6 “Popper on Demarcation and Induction” (1974)
- 3.7 “Why Did Copernicus’s Research Programme Supersede Ptolemy’s?” (1976)
- 4. Mincemeat Unmade: Lakatos versus Feyerabend
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Life
1.1 A Tale of Two Lakatoses
Imre Lakatos was a warm and witty friend and a charismatic and inspiring teacher ( Feyerabend 1975a). He was also a fallibilist, and a professed foe of elitism and authoritarianism, taking a dim view of what he described as the Wittgensteinian “thought police” (owing to the Orwellian tendency on the part of some Wittgensteinians to suppress dissent by constricting the language, dismissing the stuff that they did not like as inherently meaningless) (UT: 225 and 228–36). In the later (and British) phase of his career he was a dedicated opponent of Marxism who played a prominent part in opposing the socialist student radicals at the LSE in 1968, arguing passionately against the politicization of scholarship (LTD; Congden 2002).
But in the earlier and Hungarian phase of his life, Lakatos was a Stalinist revolutionary, the leader of a communist cell who persuaded a young comrade that it was her duty to the revolution to commit suicide, since otherwise she was likely to be arrested by the Nazis and coerced into betraying the valuable young cadres who constituted the group (Bandy 2009: ch. 5; Long 1998 and 2002; Congden 1997). So far from being a fallibilist, the young Lakatos displayed a cocksure self-confidence in his grasp of the historical situation, enough to exclude any alternative solution to the admittedly appalling problems that this group of young and mostly Jewish communists were facing in Nazi-occupied Hungary. (“Is there no other way?” the young comrade asked. The answer, apparently, was “No”: Long 2002: 267.) After the Soviet victory, during the late 1940s, he was an eager co-conspirator in the creation of a Stalinist state, in which the denunciation of deviationists was the order of the day (Bandy 2009: ch. 9). Lakatos was something close to a thought policeman himself, with a powerful job in the Ministry of Education, vetting university teachers for their political reliability (Bandy 2009: ch. 8; Long 2002: 272–3; Congden 1997). Later on, after falling afoul of the regime that he had helped to establish and doing time in a gulag at Recsk, he served the ÁVH, the Hungarian secret police, as an informant by keeping tabs on his friends and comrades (Bandy 2009: ch. 14; Long 2002). And he took a prominent part, as a Stalinist student radical, in trying to purge the University of Debrecen of “reactionary” professors and students and in undermining the prestigious but unduly independent Eötvös College, arguing passionately against the depoliticized (but covertly bourgeois) scholarship that Eötvös allegedly stood for (Bandy 2009: chs. 4 and 9; Long 1998 and 2002).
1.2 Life and Works: The Second World and the Third
To the many that knew and loved the later Lakatos, some of these facts are difficult to digest. But how relevant are they to assessing his philosophy, which was largely the product of his British years? This is an important question as Lakatos was wont to draw a Popperian distinction between World 3—the world of theories, propositions and arguments—and World 2—the psychological world of beliefs, decisions and desires. And he was sometimes inclined to suggest that in assessing a philosopher’s work we should confine ourselves to World 3 considerations, leaving the subjectivities of World 2 to one side (F&AM: 140).
So does a philosopher’s life have any bearing on his works? We take our cue from the writings of Lakatos himself. Of course, there were facts about his early career that Lakatos would not have wanted to be widely known, and which he managed to keep concealed from his Western friends and colleagues during his lifetime. But what does his official philosophy have to say about the relevance of biographical data to intellectual history?
In “The History of Science and its Rational Reconstructions” (HS&IRR) Lakatos develops a theory of how to do the history of science, which, with some adjustments, can be blown up into an account of how to do intellectual history in general. For Lakatos, the default assumption in the history of science is that the scientists in question are engaged in a more-or-less rational effort to solve a set of (relatively) “pure” problems (such as “How to explain the apparent motions of the heavenly bodies consistently with a plausible mechanics?”). A “rational reconstruction” in the history of science, employs a theory of (scientific) rationality in conjunction with an account of the problems as they appeared to the scientists in question to display some intellectual episode as a series of rational responses to the problem-situation. On the whole, it is a plus for a theory of [scientific] rationality if it can display the history of science as a relatively rational affair and a strike against it if it cannot. Thus in Lakatos’s opinion, naïve versions of Popper’s falsificationism are in a sense falsified by the history of science, since they represent too much of it as an irrational affair with too many scientists hanging on to hypotheses that they ought to have recognized as refuted. If the rational reconstruction succeeds—that is if we can display some intellectual development as a rational response to the problem situation—then we have an “internal” history of the developments in question. If not, then the “rational reconstruction of history needs to be supplemented by an empirical (socio-psychological) ‘external history’” (HS&IRR: 102). Non-rational or “external” factors sometimes interfere with the rational development of science. “No rationality theory will ever solve problems like why Mendelian genetics disappeared in Soviet Russia in the 1950s” [the reason being that Lysenko, a Stalin favourite, acquired hegemonic status within the world of Soviet biology and persecuted the Mendelians] (HS&IRR: 114).
(Perhaps this marks an important departure from Hegel. For a true Hegelian, everything can, in the last analysis, be seen as rationally required for the self-realization of the Absolute. Hence all history is “internal” in something like Lakatos’s sense, since the “cunning of reason” ensures that apparently irrational impulses are subordinated to the ultimate goal of history.)
Is there, so to speak, an “internal” history of Lakatos’s intellectual development that can be displayed as rational? Or must it be partly explained in terms of “external” influences? The answer depends on the account of rationality that we adopt and the problem situation that we take him to have been addressing.
Whether or not a particular theoretical (or practical) choice is susceptible to an internal explanation depends, in part, on the actor’s problem. Consider, for example, Descartes’ theory of the vortices, namely that the planets are whirled round the sun by a fluid medium which itself contains little whirlpools in which the individual planets are swimming. Descartes’ theory of the vortices, is fairly rational if we take it as an attempt (in the light of what was then known) to explain the motion of the heavenly bodies in a way that is consistent with Copernican astronomy. But it is a lot more rational if we take to be an attempt to explain the motion of the heavenly bodies in a way that is consistent with Copernican astronomy without formally contradicting the Church’s teaching that the earth does not move. (The earth goes round the sun but it does not move with respect to the fluid medium that whirls it round the sun, and, for Descartes, motion is defined as motion with respect to the contiguous matter.) So do we read Descartes’ theory as a fairly rational attempt to solve one problem which is distorted by an external factor or as a very rational attempt solve a related but more complex problem? Well the answer may not be clear, but if we want to understand Descartes intellectual development we need to know that it was an important constraint on his theorizing that his views should be formally consistent with the doctrines of the Church.
Similarly, it is important in understanding Lakatos’s theorizing to realize (for example) that in later life he wanted to develop a demarcation criterion between science and non-science that left Soviet Marxism (though not perhaps all forms of Marxism) on the non-scientific side of the divide. And this holds whether we regard this constraint as a non-rational external factor or as a constituent of his problem situation and hence internal to a rational reconstruction of his intellectual development. Biographical facts can be relevant to understanding a thinker’s ideas since they can help to illuminate the problem situation to which they were addressed.
Furthermore, the big issue with respect to Lakatos’s development is how much of the old Hegelian-Marxist remained in the later post-Popperian philosopher, and how much of his philosophy was a reaction against his earlier self. To answer this question we need to know something about that earlier self—either the self that secretly persisted or the self that the later Lakatos was reacting against.
1.3 From Stalinist Revolutionary to Methodologist of Science
Imre Lakatos was born Imre Lipsitz in Debrecen, eastern Hungary, on November 9, 1922, the only child of Jewish parents, Jacob Marton Lipsitz and Margit Herczfeld. Lakatos’s parents parted when he was very young and he was largely brought up by his grandmother and his mother who worked as a beautician. The Hungary into which Lakatos was born was a kingdom without a king ruled by an admiral without a navy, the “Regent” Admiral Horthy, who had gained his naval rank in the service of the then-defunct Austro-Hungarian Empire. The regime was authoritarian, a sort of fascism-lite. After a brilliant school career, during which he won mathematics competitions and a multitude of prizes, Lakatos entered Debrecen University in 1940. Lakatos graduated in Physics, Mathematics, and Philosophy in 1944. During his time at Debrecen he became a committed communist, attending illegal underground communist meetings and, in 1943, starting his own illegal study group.
No-one who attended Imre’s groups has forgotten the intensity and brilliance of the atmosphere. “He opened the world to me!” a participant said. Even those who were later disillusioned with communism or ashamed of acts they committed, remember the sense of inspiration, clear thinking and hope for a new society they felt in Imre’s secret seminars. (Long 2002: 265)
However, in Lakatos’s group the emphasis was on preparing the young cadres for the coming communist revolution, rather than engaging in public propaganda or antifascist resistance activities (Bandy 2009: ch. 3).
In March 1944 the Germans invaded Hungary to forestall its attempts to negotiate a separate peace. (The Hungarian government had allied with the Axis powers, in the hopes of recovering some of the territories lost at the Treaty of Trianon in 1920. By 1944 they had begun to realize that this was a mistake.) Admiral Horthy, whose anti-Semitism was a more gentlemanly affair than that of the Nazis (he was fine with systematic discrimination but apparently drew the line at mass-murder), was forced to accept a collaborationist government led by Döme Sztójay as prime minister. The new regime had none of Horthy’s humanitarian scruples and began a policy of enthusiastic and systematic cooperation with the Nazi genocide program. In May, Lakatos’s mother, grandmother and other relatives were forced into the Debrecen ghetto, thence to die in Auschwitz—the fate of about 600,000 Hungarian Jews. Lakatos’s father, a wine merchant, managed to get away and survived the war, eventually ending up in Australia. A little earlier, in March, Lakatos himself had managed to escape from Debrecen to Nagyvárad (now Oradea in Romania) with false papers under the name of Molnár. Later, a Hungarian friend, Vilma Balázs, recalled that
Imre [had been] very close to his mother and they were quite poor. He often blamed himself for her death and wondered if he could have saved her (Bandy 2009: 32).
In Nagyvárad Lakatos restarted his Marxist group. The co-leader was his then-girlfriend and subsequent wife, Éva Révész. In May, the group was joined by Éva Izsák, a 19-year-old Jewish antifascist activist who needed lodgings with a non-Jewish family. Lakatos decided that there was a risk that she would be captured and forced to betray them, hence her duty, both to the group and to the cause, was to commit suicide. A member of the group took her across country to Debrecen and gave her cyanide (Congden 1997, Long 2002, Bandy 2009, ch. 5). To lovers of Russian literature, the episode recalls Dostoevsky’s The Possessed/Demons (based in part on the real-life Nechaev affair). In Dostoevsky’s novel the anti-Tsarist revolutionary, Pyotr Verkhovensky, posing as the representative of a large revolutionary organization, tries to solidify the provincial cell of which he is the chief by getting the rest of group to share in the murder of a dissident member who supposedly poses a threat to the group. (It does not work for the fictional Pytor Verkhovensky and it did work for the real-life Sergei Nechaev.) Hence the title of Congden’s 1997 exposé: “Possessed: Imre Lakatos’s Road to 1956”. But to communists or former communists of Lakatos’s generation, it recalled a different book: Chocolate, by the Bolshevik writer Aleksandr Tarasov-Rodianov. This is a stirring tale of revolutionary self-sacrifice in which the hero is the chief of the local Cheka (the forerunner of the KGB). Popular in Hungary, it encouraged a romantic cult of revolutionary ruthlessness and sacrifice in its (mostly) youthful readers. As one of Lakatos’s contemporaries, György Magosh put it,
How that book inspired us. How we longed to be professional revolutionaries who could be hanged several times a day in the interest of the working class and of the great Soviet Union (Bandy 2009: 31).
It was in that spirit, that the ardent young Marxist, Éva Izsák, could be persuaded that it was her duty to kill herself for the sake of the cause. As for Lakatos himself, a chance remark in his most famous paper suggests something about his attitude.
One has to appreciate the dare-devil attitude of our methodological falsificationist [or perhaps as he would have said in an earlier phase of his career, the conscientious Leninist]. He feels himself to be a hero who, faced with two catastrophic alternatives, dares to reflect coolly on their relative merits and [to] choose the lesser evil. (FMSRP: 28)
If you admire the hero who has the courage to make the tough choice between two catastrophic alternatives, isn’t there a temptation to manufacture catastrophic alternatives so that you can heroically choose between them?
Late in 1944, following a Soviet victory, Lakatos returned to Debrecen, and changed his name from the Germanic Jewish Lipsitz to the Hungarian proletarian Lakatos (meaning “locksmith”). He became active in the now legal Communist Party and in two leftist youth and student organizations, the Hungarian Democratic Youth Federation (MADISZ) and the Debrecen University Circle (DEK). As one of the leaders of the DEK, Lakatos agitated for the dismissal of reactionary professors from Debrecen and the exclusion of reactionary students.
We are aware that this move on our part is incompatible with the traditional and often voiced “autonomy” of the university [Lakatos stated], but respect for autonomy, in our view, cannot mean that we have to tolerate the strengthening of fascism and reaction (Bandy 2009: 59 and 61).
Lakatos moved to Budapest in 1946. He became a graduate student at Budapest University, but spent much of his time working towards the communist takeover of Hungary. This was a slow-motion affair, characterized by the infamous “salami tactics” of the Communist leader Mátyás Rákosi. Lakatos worked chiefly in the Ministry of Education, evaluating the credentials of university teachers and making lists of those who should be dismissed as untrustworthy once the communists had taken over (Bandy 2009: ch. 8). He was also a student at Eötvös College, but attacked it publicly as an elitist and bourgeois institution. The College, and others like it, was closed in 1950 after the communist takeover. In 1947 Lakatos gained his doctorate from Debrecen University for a thesis entitled “On the Sociology of Concept Formation in the Natural Sciences”. In 1948, after the communist takeover was substantially complete, he gained a scholarship to undertake further study in Moscow.
Lakatos flew to Moscow in January 1949, only to be recalled for “un-Party-like” behaviour in July. What these “un-party-like” activities were is something of a mystery but even more of a mystery is why, having returned from Moscow under a cloud, he seemed so cool, calm and collected. Lakatos’s biographers, Long and Bandy, speculate that he was being held in reserve to prepare a case against the communist education chief, József Révai, who was scheduled to appear in a new show trial. But when Rákosi decided not to prosecute Révai after all, Lakatos was thrown to the wolves (Bandy 2009: ch. 12; Long 2002). He was arrested in April 1950 on charges of revisionism and, after a period in the cellars of the secret police (including, of course, torture), he was condemned to the prison camp at Recsk.
However Lakatos was probably doomed anyway. In later life Lakatos was big admirer of Orwell’s Nineteen Eighty-Four. Perhaps he recognized himself in Orwell’s description of the Party intellectual (and expert on Newspeak) Syme:
Unquestionably Syme will be vaporized, Winston thought again. He thought it with a kind of sadness, although well knowing that Syme…was fully capable of denouncing him as a thought-criminal if he saw any reason for doing so. There was something subtly wrong with Syme. There was something that he lacked: discretion, aloofness, a sort of saving stupidity. You could not say that he was unorthodox. He believed in the principles of Ingsoc, he venerated Big Brother, he rejoiced over victories, he hated heretics…. Yet a faint air of disreputability always clung to him. He said things that would have been better unsaid, he had read too many books…. (Orwell 2008 [1949]: 58)
An instance of Lakatos’s Syme-like behaviour is his 1947 denunciation of the literary critic and philosopher György Lukács, one of the intellectual luminaries of the communist movement. Lukács represented the academically respectable face of communism, and favoured a gradual and democratic transition to the dictatorship of the proletariat. Lakatos organized an “anti-Lukács meeting…held under the aegis of the Valóság Circle” to critique Lukács’s foot-dragging and “Weimarism” (Bandy 2009: 110). Once the regime was firmly in control, Lukács was indeed censured for his undue concessions to bourgeois democracy, and he spent the early fifties under a cloud. But in 1947, Lakatos’s criticisms were deemed premature and he got into trouble because of his un-Party-like activities. (Lukács himself referred to the episode as a “cliquish kaffe klatsch”.) In Communist Hungary it was important not to be “one pamphlet behind” the Party line (Bandy 2009: 92). Lakatos was the sort of over-zealous communist who was sometimes a couple of pamphlets ahead.
After his release from Recsk in September 1953 (minus several teeth), Lakatos remained for a while, a loyal Stalinist. He eked out a living in the Mathematics Institute of the Hungarian Academy of Science, reading, researching and translating (including a translation into Hungarian of George Pólya’s How to Solve It). During this time he was informing on friends and colleagues to the ÁVH, the Hungarian secret police, though he subsequently claimed that he did not pass on anything incriminating (Long, 2002: 290 ). It was whilst working at the Mathematics Institute that he first gained access to the works of Popper. Gradually he turned against the Stalinist Marxism that had been his creed. He married (as his second wife) Éva Pap and lived at her parents’ house (his father-in-law being the distinguished agronomist, Endre Pap). In 1956 he joined the revisionist Petőfi Circle and delivered a stirring speech on “On Rearing Scholars” which at least burnt his bridges with Stalinism:
The very foundation of scholarly education is to foster in students and postgrads a respect for facts, for the necessity of thinking precisely, and to demand proof. Stalinism, however, branded this as bourgeois objectivism. Under the banner of partinost [Party-like] science and scholarship, we saw a vast experiment to create a science without facts, without proofs.
… a basic aspect of the rearing of scholars must be an endeavour to promote independent thought, individual judgment, and to develop conscience and a sense of justice. Recent years have seen an entire ideological campaign against independent thinking and against believing one’s own senses. This was the struggle against empiricism [Laughter and applause] (Bandy 2009: 221. Bandy quotes the transcripts which seem to differ slightly from the prepared text in the Lakatos archives, reprinted in F&AM)
But Lakatos was not just explicitly repudiating Stalinism. He was also implicitly criticizing another prominent member of the Petőfi Circle who had been a big influence on his first PhD, namely György Lukács. (See Ropolyi 2002 for the early influence.) For Lukács’s work is pervaded by just the kind of hostility towards empiricism and disdain for facts that Lakatos is denouncing in his speech, as well as an arts-sider’s contempt for the natural sciences, all of which would have been anathema to the later Lakatos. Indeed Lukács was notorious for the view that that
even if the development of science had proved all Marx’s assertions to be false…we could accept this scientific criticism without demur and still remain Marxists—as long as we adhered to the Marxist method
and that
the orthodox Marxist who realizes that…the time has come for the expropriation of the exploiters, will respond to the vulgar-Marxist litany of “facts” which contradict this process with the words of Fichte, one of the greatest of classical German philosophers: “So much the worse for the facts”. (Lukács 2014 [1919]: ch. 3.)
Thus the Stalinist Lakatos of 1947 had explicitly denounced Lukács for not being Stalinist enough, but the revisionist Lakatos of 1956 was implicitly denouncing Lukács for being methodologically too much of a Stalinist. For the later Lakatos, what was wrong with “orthodox Marxism” was chiefly that its novel factual predictions had been systematically falsified (see §3.2 below). But that was pretty much the complaint of early revisionists such as Bernstein (see Kolakowski 1978: ch. 4) and it was against that kind of revisionism that Lukács’s Bolshevik writings were a protest. (See Lukács 1971 [1923] and 2014 [1919].) Though factual “refutations” of a research programme are not always decisive, a Lukács-like indifference to the facts is, for Lakatos, the mark of a fundamentally unscientific attitude. In our opinion, this puts paid to Ropolyi’s claim that Lukács continued to be a major influence on the later Lakatos.
Lakatos left Hungary in November 1956 after the Soviet Union crushed the short-lived Hungarian revolution. He walked across the border into Austria with his wife and her parents. Within two months he was at King’s College Cambridge, with a Rockefeller Fellowship to write a PhD under the supervision of R.B. Braithwaite, which he completed in 1959 under the title “Essays in the Logic of Mathematical Discovery”. If we set aside his romantic adventures, the story of Lakatos’s life thereafter is largely the story of his work, though we should not forget his activities as an academic politician. Even his friendship with Feyerabend and his friendship and subsequent bust-up with Popper were very much work-related. In Britain his academic career was meteoric. In 1960 he was appointed Assistant Lecturer in Karl Popper’s department at the London School of Economics. By 1969 he was Professor of Logic, with a worldwide reputation as a philosopher of science. During the student revolts of the 1960s, which in Britain were centred on the LSE, Lakatos became an establishment figure. He wrote a “Letter to the Director of the London School of Economics” defending academic freedom and academic autonomy, which was widely circulated. It denounces the student radicals for allegedly trying to do what he himself had done at Debrecen and Eötvös (though he was careful to conceal the parallel, citing Nazi and Muscovite precedents instead) (LTD: 247).
Lakatos died suddenly in 1974 of a heart attack at the height of his powers. He was 51.
2. Lakatos’s Big Ideas
Imre Lakatos has two chief claims to fame.
2.1 Against Formalism in Mathematics
The first is his Philosophy of Mathematics, especially as set forth in “Proofs and Refutations” (1963–64) a series of four articles, based on his PhD thesis, and written in the form of a many-sided dialogue. These were subsequently combined in a posthumous book and published, with additions, in 1976. The title is an allusion to a famous paper of Popper’s, “Conjectures and Refutations” (the signature essay of his best-known collection), in which Popper outlines his philosophy of science. Lakatos’s point is that the development of mathematics is much more like the development of science as portrayed by Popper than is commonly supposed, and indeed much more like the development of science as portrayed by Popper than Popper himself supposed.
What Lakatos does not make so much of (though he does not conceal it either) is that in his view the development of mathematics is also much more like the development of thought in general as analysed by Hegel than Hegel himself supposed. There is thesis, antithesis and synthesis, “Hegelian language, which [Lakatos thinks would] generally be capable of describing the various developments in mathematics” (P&R: 146). Thus there is a certain sense in which Lakatos out-Hegels Hegel, giving a dialectical analysis of a discipline (mathematics) that Hegel himself despised as insufficiently dialectical (see Larvor 1998, 1999, 2001). Hence Feyerabend’s gibe (which Lakatos took in good part) that Lakatos was a Pop-Hegelian, the bastard child of Popperian father and a Hegelian mother (F&AM: 184–185).
Proofs and Refutations is a critique of “formalist” philosophies of mathematics (including formalism proper, logicism and intuitionism), which, in Lakatos’s view, radically misrepresent the nature of mathematics as an intellectual enterprise. For Lakatos, the development of mathematics should not be construed as series of Euclidean deductions where the contents of the relevant concepts has been carefully specified in advance so as to preclude equivocation. Rather, these water-tight deductions from well-defined premises are the (perhaps temporary) end-points of an evolutionary, and indeed a dialectical, process in which the constituent concepts are initially ill-defined, open-ended or ambiguous but become sharper and more precise in the context of a protracted debate. The proofs are refined in conjunction with the concepts (hence “proof-generated concepts”) whilst “refutations” in the form of counterexamples play a prominent part in the process. [One might almost say, paraphrasing Hegel, that in Lakatos’s view “when Euclidean demonstrations paint their grey in grey, then has a shape of mathematical life grown old…The owl of the formalist Minerva begins its flight only with the falling of dusk” (Hegel 2008 [1820/21]: 16).]
Lakatos is also keen to display the development of mathematics as a rational affair even though the proofs (to begin with) are often lacking in logical rigour and the key concepts are often open-ended and unclear
The idea—expressed so clearly by Seidel [and clearly endorsed by Lakatos himself]—that a proof can be respectable without being flawless, was a revolutionary one in 1847, and, unfortunately, still sounds revolutionary today. (P&R: 139)
A corollary of this is that in mathematics many of the “proofs” are not really proofs in the full sense of the word (that is, demonstrations that proceed deductively from apodictic premises via unquestionable rules of inference to certain conclusions) and that many of the “refutations” are not really refutations either, since something rather like the “refuted” thesis often survives the refutation and arises refreshed and invigorated from the dialectical process.
This becomes apparent early on in the dialogue, when the Popperian Gamma protests at the Teacher’s insouciance with respect to refutation, a counterexample to Euler’s thesis (and therefore to Cauchy’s proof) that, for all regular polyhedra, the number of vertices, minus the number of edges, plus the number of faces equals two. The counterexample is a solid bounded by a pair of nested cubes, one of which is inside, but does not touch the other:
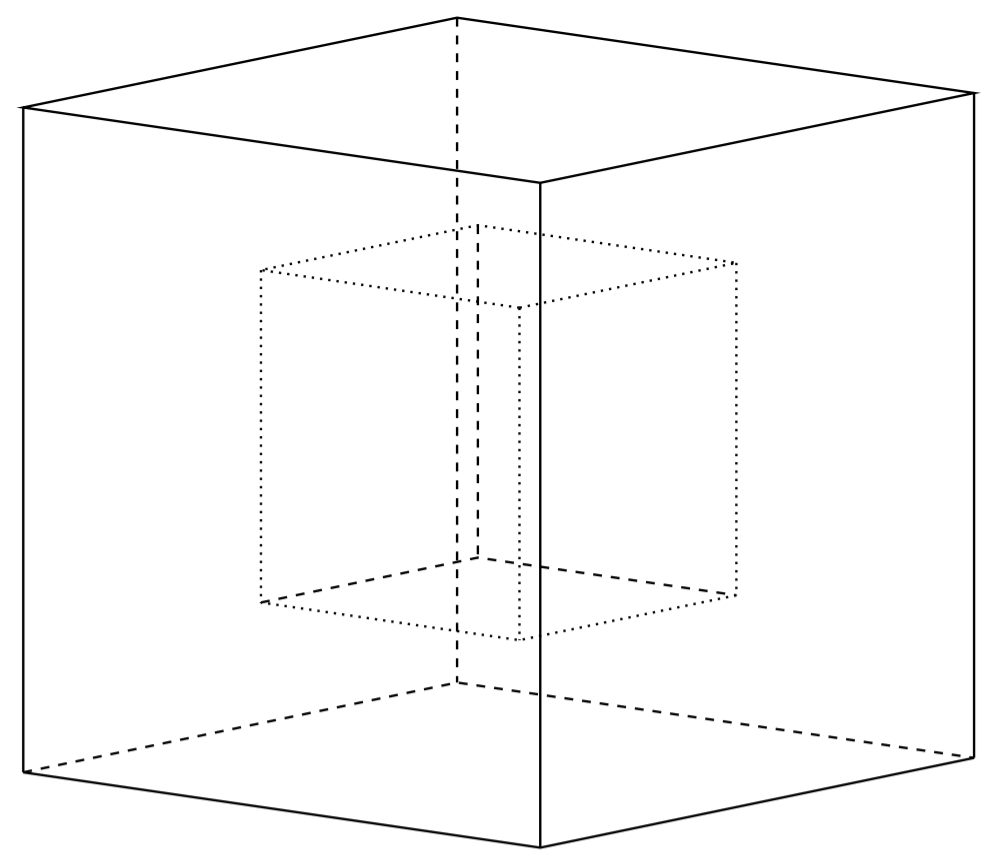
For this hollow cube, \(V - E + F\) (including both the inner and the outer ones) \(= 4\). According to Gamma, this simply refutes Euler’s conjecture and disproves Cauchy’s proof:
GAMMA: Sir, your composure baffles me. A single counterexample refutes a conjecture as effectively as ten. The conjecture and its proof have completely misfired. Hands up! You have to surrender. Scrap the false conjecture, forget about it and try a radically new approach.
TEACHER: I agree with you that the conjecture has received a severe criticism by Alpha’s counterexample. But it is untrue that the proof has “completely misfired”. If, for the time being, you agree to my earlier proposal to use the word “proof” for a “thought-experiment which leads to decomposition of the original conjecture into subconjectures”, instead of using it in the sense of a “ guarantee of certain truth”, you need not draw this conclusion. My proof certainly proved Euler’s conjecture in the first sense, but not necessarily in the second. You are interested only in proofs which “prove” what they have set out to prove. I am interested in proofs even if they do not accomplish their intended task. Columbus did not reach India but he discovered something quite interesting.
Thus even in his earlier work, when he is still a professed disciple of Popper, Lakatos is already a rather dissident Popperian. Firstly, there are the hat-tips to Hegel as well as to Popper that crop up from time to time in Proofs and Refutations including the passage where he praises (and condemns) them both in the same breath. (“Hegel and Popper represent the only fallibilist traditions in modem philosophy, but even they both made the mistake of reserving a privileged infallible status for mathematics”. P&R: 139n.1.) Given that Hegel was anathema to Popper (witness his famous or notorious anti-Hegel “scherzo” in The Open Society and Its Enemies, (1945 [1966])) this strongly suggests that Lakatos took his Popper with a large pinch of salt. Secondly, for Popper himself a proof is a proof and a refutation is supposed to kill a scientific conjecture stone-dead. Thus non-demonstrative proofs and non-refuting refutations mark a major departure from Popperian orthodoxy.
2.2 Improving on Popper in the Philosophy of Science
The dissidence continues with Lakatos’s second major contribution to philosophy, his “Methodology of Scientific Research Programmes” or MSRP (developed in detail in in his FMSRP), a radical revision of Popper’s Demarcation Criterion between science and non-science, leading to a novel theory of scientific rationality. This is arguably a lot more realistic than the Popperian theory it was designed to supplant (or, in earlier formulations, the Popperian theory that it was designed to amend). For Popper, a theory is only scientific if is empirically falsifiable, that is if it is possible to specify observation statements which would prove it wrong. A theory is good science, the sort of theory you should stick with (though not the sort of thing you should believe since Popper did not believe in belief), if it is refutable, risky, and problem-solving and has stood up to successive attempts at refutation. It must be highly falsifiable, well-tested but (thus far) unfalsified.
Lakatos objects that although there is something to be said for Popper’s criterion, it is far too restrictive, since it would rule out too much of everyday scientific practice (not to mention the value-judgments of the scientific elite) as unscientific and irrational. For scientists often persist—and, it seems, rationally persist—with theories, such as Newtonian celestial mechanics that by Popper’s standards they ought to have rejected as “refuted”, that is theories that (in conjunction with other assumptions) have led to falsified predictions. A key example for Lakatos is the “Precession of Mercury” that is, the anomalous behaviour of the perihelion of Mercury, which shifts around the Sun in a way that it ought not to do if Newton’s mechanics were correct and there were no other sizable body influencing its orbit. The problem is that there seems to be no such body. The difficulty was well known for decades but it did not cause astronomers to collectively give up on Newton until Einstein’s theory came along. Lakatos thought that the astronomers were right not to abandon Newton even though Newton eventually turned out to be wrong and Einstein turned out to be right.
Again, Copernican heliocentric astronomy was born “refuted” because of the apparent non-existence of stellar parallax. If the earth goes round the sun then the apparent position of at least some of the fixed stars (namely the closest ones) ought to vary with respect to the more distant ones as the earth is moving with respect to them. Some parts of the night sky should look a little different at perihelion (when the earth is furthest from the sun) from the way that they look at aphelion (when the earth is at its nearest to the sun, and hence at the other end of its orbit). But for nearly three centuries after the publication of Copernicus’ De Revolutionibus 1543, no such differences were observed. In fact, there is a very slight difference in the apparent positions of the nearest stars depending on the earth’s position in its orbit, but the difference is so very slight as to be almost undetectable. Indeed it was completely undetectable until 1838 when sufficiently powerful telescopes and measuring techniques were able to detect it, by which time the heliocentric view had long been regarded as an established fact. Thus astronomers had not given up on either Copernicus or his successors despite this apparent falsification.
But if scientists often persist with “refuted” theories, either the scientists are being unscientific or Popper is wrong about what constitutes good science, and hence about what scientists ought to do. Lakatos’s idea is to construct a methodology of science, and with it a demarcation criterion, whose precepts are more in accordance with scientific practice.
How does it work? Well, falsifiability continues to play a part in Lakatos’s conception of science but its importance is somewhat diminished. Instead of an individual falsifiable theory which ought to be rejected as soon as it is refuted, we have a sequence of falsifiable theories characterized by shared a hard core of central theses that are deemed irrefutable—or, at least, refutation-resistant—by methodological fiat. This sequence of theories constitutes a research programme.
The shared hard core of this sequence of theories is often unfalsifiable in two senses of the term.
Firstly scientists working within the programme are typically (and rightly) reluctant to give up on the claims that constitute the hard core.
Secondly the hard core theses by themselves are often devoid of empirical consequences. For example, Newtonian mechanics by itself—the three laws of mechanics and the law of gravitation—won’t tell you what you will see in the night sky. To derive empirical predictions from Newtonian mechanics you need a whole host of auxiliary hypotheses about the positions, masses and relative velocities of the heavenly bodies, including the earth. (This is related to Duhem’s thesis that, generally speaking, theoretical propositions—and indeed sets of theoretical propositions—cannot be conclusively falsified by experimental observations, since they only entail observation-statements in conjunction with auxiliary hypotheses. So when something goes wrong, and the observation statements that they entail turn out to be false, we have two intellectual options: modify the theoretical propositions or modify the auxiliary hypotheses. See Ariew 2014.) For Lakatos an individual theory within a research programme typically consists of two components: the (more or less) irrefutable hard core plus a set of auxiliary hypotheses. Together with the hard core these auxiliary hypotheses entail empirical predictions, thus making the theory as a whole—hard core plus auxiliary hypotheses—a falsifiable affair.
What happens when refutation strikes, that is when the hard core in conjunction with the auxiliary hypotheses entails empirical predictions which turn out to be false? What we have essentially is a modus tollens argument in which science supplies one of the premises and nature (plus experiment and observation) supplies the other:
- If <hard core plus auxiliary hypotheses>, then O (where O represents some observation statement);
- Not-O (Nature shouts “no”: the predictions don’t pan out);
Therefore
- Not <hard core plus auxiliary hypotheses>.
But logic leaves us with a choice. The conjunction of the hard core plus the auxiliary hypotheses has to go, but we can retain either the hard core or the auxiliary hypotheses. What Lakatos calls the negative heuristic of the research programme, bids us retain the hard core but modify the auxiliary hypotheses:
The negative heuristic of the programme forbids us to direct the modus tollens at this “hard core”. Instead, we must use our ingenuity to articulate or even invent “auxiliary hypotheses”, which form a protective belt around this core, and we must redirect the modus tollens to these. It is this protective belt of auxiliary hypotheses which has to bear the brunt of tests and gets adjusted and re-adjusted, or even completely replaced, to defend the thus-hardened core. (FMSRP: 48)
Thus when refutation strikes, the scientist constructs a new theory, the next in the sequence, with the same hard core but a modified set of auxiliary hypotheses. How is she supposed to do this? Well, associated with the hard core, there is what Lakatos calls the positive heuristic of the programme.
The positive heuristic consists of a partially articulated set of suggestions or hints on how to change, develop the “refutable variants” of the research programme, how to modify, sophisticate, the “refutable” protective belt. (FMSRP: 50)
For example, if a planet is not moving in quite the smooth ellipse that it ought to follow a) if Newtonian mechanics were correct and b) if there were nothing but the sun and the planet itself to worry about, then the positive heuristic of the Newtonian programme bids us look for another heavenly body whose gravitational force might be distorting the first planet’s orbit. Alternatively, if stellar parallax is not observed, we can try to refute this apparent refutation by refining our instruments and making more careful measurements and observations.
Lakatos evidently thinks that when one theory in the sequence has been refuted, scientists can legitimately persist with the hard core without being in too much of a hurry to construct the next refutable theory in the sequence. The fact that some planetary orbits are not quite what they ought to be should not lead us to abandon Newtonian celestial mechanics, even if we don’t yet have a testable theory about what exactly is distorting them. It is worth remarking too that the auxiliary hypotheses play a rather paradoxical part in Lakatos’s methodology. On the one hand, they connect the central theses of the hard core with experience, allowing to them to figure in testable, and hence, refutable theories. On the other hand, they insulate the theses of the hard core from refutation, since when the arrow of modus tollens strikes, we direct it at the auxiliary hypotheses rather than the hard core.
So far we have had an account of what scientists typically do do and what Lakatos thinks that they ought to do. But what about the Demarcation Criterion between science and non-science or between good science and bad? Even if it is sometimes rational to persist with the hard core of a theory when the hard core plus some set of auxiliary hypotheses has been refuted, there must surely be some circumstances in which is it rational to give it up! The Methodology of Scientific Research Programme has got to be something more than a defence of scientific pig-headedness! As Lakatos himself puts the point:
Now, Newton’s theory of gravitation, Einstein’s relativity theory, quantum mechanics, Marxism, Freudianism [the last two stock examples of bad science or pseudo-science for Popperians], are all research programmes, each with a characteristic hard core stubbornly defended, each with its more flexible protective belt and each with its elaborate problem-solving machinery. Each of them, at any stage of its development, has unsolved problems and undigested anomalies. All theories, in this sense, are born refuted and die refuted. But are they [all] equally good? (S&P: 4–5.)
Lakatos, of course, thinks not. Some science is objectively better than other science and some science is so unscientific as to hardly qualify as science at all. So how does he distinguish between “a scientific or progressive programme” and a “pseudoscientific or degenerating one”? (S&P: 4–5.)
To begin with, the unit of scientific evaluation is no longer the individual theory (as with Popper), but the sequence of theories, the research programme. We don’t ask ourselves whether this or that theory is scientific or not, or whether it constitutes good or bad science. Rather we ask ourselves whether the sequence of theories, the research programme, is scientific or non-scientific or constitutes good or bad science. Lakatos’s basic idea is that a research programme constitutes good science—the sort of science it is rational to stick with and rational to work on—if it is progressive, and bad science—the kind of science that is, at least, intellectually suspect—if it is degenerating. What is it for a research programme to be progressive? It must meet two conditions. Firstly it must be theoretically progressive. That is, each new theory in the sequence must have excess empirical content over its predecessor; it must predict novel and hitherto unexpected facts (FMSRP: 33). Secondly it must be empirically progressive. Some of that novel content has to be corroborated, that is, some of the new “facts” that the theory predicts must turn out to be true. As Lakatos himself put the point, a research programme “is progressive if it is both theoretically and empirically progressive, and degenerating if it is not” (FMSRP: 34). Thus a research programme is degenerating if the successive theories do not deliver novel predictions or if the novel predictions that they deliver turn out to be false.
Novelty is, in part, a comparative notion. The novelty of a research programme’s predictions is defined with respect to its rivals. A prediction is novel if the theory not only predicts something not predicted by the previous theories in the sequence, but if the predicted observation is predicted neither by any rival programme that might be in the offing nor by the conventional wisdom. A programme gets no brownie points by predicting what everyone knows to be the case but only by predicting observations which come as some sort of a surprise. (There is some ambiguity here and some softening later on—see below §3.6—but to begin with, at least, this was Lakatos’s dominant idea.)
One of Lakatos’s key examples is the predicted return of Halley’s comet which was derived by observing part of its trajectory and using Newtonian mechanics to calculate the elongated ellipse in which it was moving. The comet duly turned up seventy-two years later, exactly where and when Halley had predicted, a novel fact that could not have been arrived at without the aid of Newton’s theory (S&P: 5). Before Newton, astronomers might have noticed a comet arriving every seventy-two years (though they would have been hard put to it to distinguish that particular comet from any others), but they could not have been as exact about the time and place of its reappearance as Halley managed to be. Newton’s theory delivered far more precise predictions than the rival heliocentric theory developed by Descartes, let alone the earth-centered Ptolemaic cosmology that had ruled the intellectual roost for centuries. That’s the kind of spectacular corroboration that propels a research programme into the lead. And it was a similarly novel prediction, spectacularly confirmed, that dethroned Newton’s physics in favour of Einstein’s. Here’s Lakatos again:
This programme made the stunning prediction that if one measures the distance between two stars in the night and if one measures the distance between them during the day (when they are visible during an eclipse of the sun), the two measurements will be different. Nobody had thought to make such an observation before Einstein’s programme. Thus, in progressive research programme, theory leads to the discovery of hitherto unknown novel facts. (S&P: 5.)
A degenerating research programme, on the other hand (unlike the theories of Newton and Einstein) either fails to predict novel facts at all, or makes novel predictions that are systematically falsified. Marxism, for example, started out as theoretically progressive but empirically degenerate (novel predictions systematically falsified) and ended up as theoretically degenerate as well (no more novel predictions but a desperate attempt to explain away unpredicted “observations” after the event).
Has…Marxism ever predicted a stunning novel fact successfully? Never! It has some famous unsuccessful predictions. It predicted the absolute impoverishment of the working class. It predicted that the first socialist revolution would take place in the industrially most developed society. It predicted that socialist societies would be free of revolutions. It predicted that there will be no conflict of interests between socialist countries. Thus the early predictions of Marxism were bold and stunning but they failed. Marxists explained all their failures: they explained the rising living standards of the working class by devising a theory of imperialism; they even explained why the first socialist revolution occurred in industrially backward Russia. They “explained” Berlin 1953, Budapest 1956, Prague 1968. They “explained” the Russian-Chinese conflict. But their auxiliary hypotheses were all cooked up after the event to protect Marxian theory from the facts. The Newtonian programme led to novel facts; the Marxian lagged behind the facts and has been running fast to catch up with them. (S&P: 4–5.)
Thus good science is progressive and bad science is degenerating and a research programme may either begin or end up as such a degenerate affair that it ceases to count as science at all. If a research programme either predicts nothing new or entails novel predictions that never come to pass, then it may have reached such a pitch of degeneration that it has transformed into a pseudoscience.
It is sometimes suggested that in Lakatos’s opinion no theory either is or ought to be abandoned, unless there is a better one in existence (Hacking 1983: 113). Does this mean that no research programme should be given up in the absence of a progressive alternative, no matter how degenerate it may be? If so, this amounts to the radically anti-sceptical thesis that it is better to subscribe to a theory that bears all the hallmarks of falsehood, such as the current representative of a truly degenerate programme, than to sit down in undeluded ignorance. (The ancient sceptics, by contrast thought that it is better not to believe anything at all rather than believe something that might be false.) We are not sure that this was Lakatos’ opinion, though he clearly thinks it a mistake to give up on a progressive research programme, unless there is a better one to shift to. But consider again the case of Marxism. What Lakatos seems to be suggesting in the passage quoted above, is that it is rationally permissible—perhaps even obligatory—to give up on Marxism even if it has no progressive rival, that is, if there is currently no alternative research programme with a set of hard core theses about the fundamental character of capitalism and its ultimate fate. (After all, the later Lakatos probably subscribed to the Popperian thesis that history in the large is systematically unpredictable. In which case there could not be a genuinely progressive programme which foretold the fate of capitalism. At best you could have a conditional theory, such as Piketty’s, which says that under capitalism, inequality is likely to grow—unless something unexpected happens or unless we decide to do something about it. See Piketty 2014: 35.) So although Lakatos thinks that the scientific community seldom gives up on a programme until something better comes along, it is not clear that he thinks that this is what they always ought to do.
There are numerous departures from Popperian orthodoxy in all this. To begin with, Lakatos effectively abandons falsifiability as the Demarcation Criterion between science and non-science. A research programme can be falsifiable (in some senses) but unscientific and scientific but unfalsifiable. First, the falsifiable non-science. Every successive theory in a degenerating research programme can be falsifiable but the programme as whole may not be scientific. This might happen if it only predicted familiar facts or if its novel predictions were never verified. A tired purveyor of old and boring truths and/or a persistent predictor of novel falsehoods might fail to make the scientific grade. Secondly, the non-falsifiable science. In Lakatos’s opinion, it need not be a crime to insulate the hard-core of your research programme from empirical refutation. For Popper, it is a sin against science to defend a refuted theory by “introducing ad hoc some auxiliary assumption, or by re-interpreting the theory ad hoc in such a way that it escapes refutation” (C&R, 48). Not so for Lakatos, though this is not to say that when it comes to ad hocery “anything goes”.
Thirdly, Lakatos’s Demarcation Criterion is a lot more forgiving than Popper’s. For a start, an inconsistent research programme need not be condemned to the outer darkness as hopelessly unscientific. This is not because any of its constituent theories might be true. Lakatos rejects the Hegelian thesis that there are contradictions in reality. “If science aims at truth, it must aim at consistency; if it resigns consistency, it resigns truth.” But though science aims at truth and therefore at consistency, this does not mean that it can’t put up with a little inconsistency along the way.
The discovery of an inconsistency—or of an anomaly—[need not] immediately stop the development of a programme: it may be rational to put the inconsistency into some temporary, ad hoc quarantine, and carry on with the positive heuristic of the programme (FMSRP: 58).
Thus it was both rational and scientific for Bohr to persist with his research programme, even though its hard core theses on the structure of the atom were fundamentally inconsistent (FMSRP: 55–58). So although Lakatos rejects Hegel’s claim that there are contradictions in reality (though not, perhaps in Reality), he also rejects Popper’s thesis that because contradictions imply everything, inconsistent theories exclude nothing and must therefore be rejected as unfalsifiable and unscientific. For Lakatos, Bohr’s theory of the atom is fundamentally inconsistent, but this does not mean that it implies that the moon is made of green cheese. Thus what Lakatos seems to be suggesting is here (though he is not as explicit as he might be) is that, when it comes to assessing scientific research programmes, we should sometimes employ a contradiction-tolerant logic; that is a logic that rejects the principle, explicitly endorsed by Popper, that anything whatever follows from a contradiction (FMSRP: 58 n. 2). In today’s terminology, Lakatos is a paraconsistentist (since he implicitly denies that from a contradiction anything follows) but not a dialetheist (since he explicitly denies that there are true contradictions). Thus he is neither a follower of Popper with respect to theories nor a follower of Hegel with respect to reality. (See Priest 2006 and 2002, especially ch. 7, and Brown and Priest 2015.)
There is another respect in which Lakatos’s Demarcation Criterion is more forgiving than Popper’s. For Popper, if a theory is not falsifiable, then it’s not scientific and that’s that. It’s an either/or affair. For Lakatos being scientific is a matter of more or less, and the more the less can vary over time. A research programme can be scientific at one stage, less scientific (or non-scientific) at another (if it ceases to generate novel predictions and cannot digest its anomalies) but can subsequently stage a comeback, recovering its scientific status. Thus the deliverances of the Criterion are matters of degree, and they are matters of degree that can vary from one time to another. We can seldom say absolutely that a research programme is not scientific. We can only say that it is not looking very scientifically healthy right now, and that the prospects for a recovery do not look good. Thus Lakatos is much more of a fallibilist than Popper. For Popper, we can tell whether a theory is scientific or not by investigating its logical implications. For Lakatos our best guesses might turn out to be mistaken, since the scientific status of a research programme is determined, in part, by its history, not just by its logical character, and history, as Popper himself proclaimed, is essentially unpredictable.
There is another divergence from Popper which helps to explain the above. Lakatos collapses two of Popper’s distinctions into one; the distinction between science and non-science and the distinction between good science and bad. As Lakatos himself put the point in his lectures at the LSE:
The demarcation problem may be formulated in the following terms: what distinguishes science from pseudoscience? This is an extreme way of putting it, since the more general problem, called the Generalized Demarcation Problem, is really the problem of the appraisal of scientific theories, and attempts to answer the question: when is one theory better than another? We are, naturally, assuming a continuous scale whereby the value zero corresponds to a pseudo-scientific theory and positive values to theories considered scientific in a higher or lesser degree. (F&AM: 20)
Apart from the fact that, for Lakatos, a) it can be rational to persist with a “falsified” theory, and indeed with theory that is actually inconsistent—both anathema to Popper—and that b) that for Lakatos “all theories are born refuted and die refuted” (S&P: 5) so that there are no unrefuted conjectures for the virtuous scientist to stick with (thus making what Popper would regard as good science practically impossible), Lakatos’s methodology of scientific research programmes replaces two of Popper’s criteria with one. For Popper has one criterion to distinguish science from non-science (or science from pseudoscience if it is a theory with scientific pretensions) and another to distinguish good science from bad science. In Popper’s view, a theory is scientific if it is empirically falsifiable and non-scientific if it is not. Being scientific or not is an absolute affair, a matter of either/or, since a theory is scientific so long as there are some observations that would falsify it. Being good science is a matter of degree, since a theory may give more or less hostages to empirical fortune, depending on the boldness of its empirical predictions. For Lakatos on the other hand, non-science or pseudo-science is at one end of a continuum with the best science at the other end of the scale. Thus a theory—or better, a research programme—can start out as genuinely scientific, gradually becoming less so over the course of time (which was Lakatos’s view of Marxism) without altogether giving up the scientific ghost. Was the Marxism of Lakatos’s day bad science or pseudo-science? From Lakatos’ point of view, the question does not have a determinate answer, the point being that it isn’t good science since it represents a degenerating research programme. But although Lakatos evidently considered Marxism to be in bad way, he could not consign it to the dustbin of history as definitively finished, since (as he often insisted) degenerating research programmes can sometimes stage a comeback.
3. Works
3.1 Proofs and Refutations (1963–4, 1976)
As we have seen, Lakatos’s first major publication in Britain was the dialogue “Proofs and Refutations” which originally appeared as a series of four journal articles. The dialogue is dedicated to George Pólya for his “revival of mathematical heuristic” and to Karl Popper for his critical philosophy.
Proofs and Refutations is a highly original production. The issues it discusses are far removed from what was then standard fare in the philosophy of mathematics, dominated by logicism, formalism and intuitionism, all attempting to find secure foundations for mathematics. Its theses are radical. And its dialogue form makes it a literary as well as a philosophical tour de force.
Its official target is “formalism” or “metamathematics”. But (as we have noted) “formalism” doesn’t just mean “formalism” proper, as this term is usually understood in the Philosophy of Mathematics. For Lakatos “formalism” includes not just Hilbert’s programme but also logicism and even intuitionism. Formalism sees mathematics as the derivation of theorems from axioms in formalised mathematical theories. The philosophical project is to show that the axioms are true and the proofs valid, so that mathematics can be seen as the accumulation of eternal truths. An additional philosophical question is what these truths are about, the question of mathematical ontology.
Lakatos, by contrast, was interested in the growth of mathematical knowledge. How were the axioms and the proofs discovered? How does mathematics grow from informal conjectures and proofs into more formal proofs from axioms? Logical empiricist (and Popperian) orthodoxy distinguished the “context of discovery” from the “context of justification”, consigned the former to the realm of empirical psychology, and thought it a matter of “unregimented insight and good fortune”, hardly a fit subject for philosophical analysis. Philosophy of mathematics consists of the logical analysis of completed theories. Formalism manifests this orthodoxy and “disconnects the history of mathematics from the philosophy of mathematics” (P&R: 1). Against the orthodoxy, Lakatos paraphrased Kant (the paraphrase has become almost as famous as the original):
the history of mathematics…has become blind, while the philosophy of mathematics… has become empty. (P&R: 2)
[Lakatos had stated this Kantian aphorism more generally at a conference in Oxford in 1961: “History of science without philosophy of science is blind. Philosophy of science without history of science is empty”. See Hanson 1963: 458.]
Suppose we agree with Lakatos that there is room for heuristics or a logic or discovery. Still, orthodoxy could insist that discovery is one thing, justification another, and that the genesis of ideas has nothing to do with their justification. Lakatos, more radically, disputed this. First, he rejected the foundationalist or justificationist project altogether: mathematics has no foundation in logic, or set theory, or anything else. Second, he insisted that the way in which a theory grows plays an essential role in its methodological appraisal. This is as much a central theme of his philosophy of empirical science as it is of his philosophy of mathematics.
As noted above, Proofs and Refutations takes the form of an imaginary dialogue between a teacher and a group of students. It reconstructs the history of attempts to prove the Descartes-Euler conjecture about polyhedra, namely, that for all polyhedra, the number of vertices minus the number of edges plus the number of faces is two (V – E + F = 2). The teacher presents an informal proof of this conjecture, due to Cauchy. This is a “thought experiment which suggest a decomposition of the original conjecture into subconjectures or lemmas” from which the original conjecture is supposed to follow. We now have, as well as the original conjecture or conclusion, the subconjectures or premises, and the meta-conjecture that the latter entail the former. Clearly, this kind of “informal proof” is quite different from the “formalist” idea that an informal proof is a formal proof with gaps (PP2: 63). Equally clearly, any of these conjectures might be refuted by counterexamples.
In the dialogue, the students, who are rather advanced, demonstrate the point—they demolish the Teacher’s “proof” by producing counterexamples. The counterexamples are of three kinds:
(1) Counterexamples to the conclusion that are not also counterexamples to any of the premises (“global but not local counterexamples”): These establish that the conclusion does not really follow from the stated premises. They require us to improve the proof, to unearth the “hidden lemma” which the counterexample also refutes, so that it becomes a “local as well as global” counterexample—see (3), below.
(2) Counterexamples to one of the premises that are not also counterexamples to the conclusion (“local but not global counterexamples”): These require us to improve the proof by replacing the refuted premise with a new premise which is not subject to the counterexample and which (we hope) will do as much to establish the conclusion as the original refuted premise did.
(3) Counterexamples both to the conclusion and to (at least one of) the premises (“global and local counterexamples”): These can be dealt with by incorporating the refuted premise or lemma into the original conclusion, as a condition of its correctness. For example, a picture-frame is a polyhedron with a hole or tunnel in it:
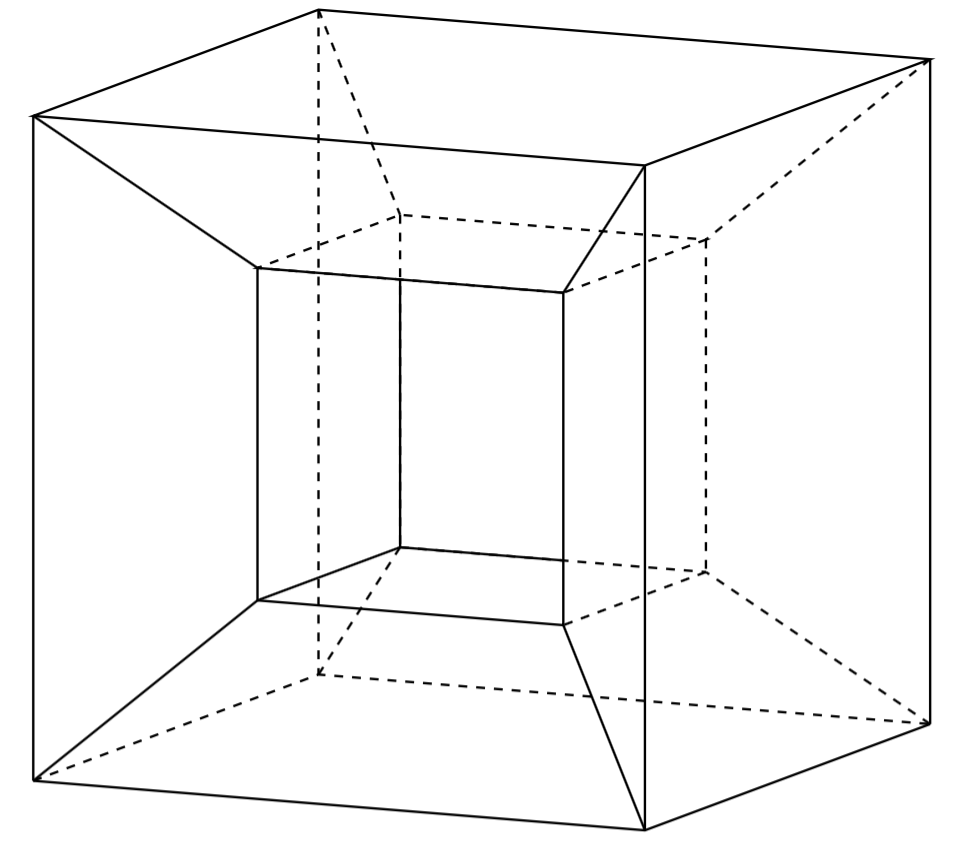
So if we define a polyhedron as “normal” if it has no holes or tunnels in it, we can restrict the original conjecture to “normal” polyhedra and avoid this refutation. The trouble with this method is that it reduces the content of the original conjecture, and an empty tautology threatens—“For all Eulerian polyhedra (polyhedra for which \(V - E + F = 2\)V – E + F = 2), V – E + F = 2\(V - E + F = 2\)”. More particularly, a blanket exclusion of polyhedra with holes or tunnels rules out some polyhedra for which \(V - E + F = 2\), despite the presence of a hole—a cube with a square hole drilled through it and two ring-shaped faces being an example – the formula V – E + F = 2 holds good. This suggests a deeper problem than finding the domain of validity of the original conjecture—finding a general relationship between V, E and F for all polyhedra whatsoever.
We see from this analysis what Lakatos calls the “dialectical unity of proofs and refutations”. Counterexamples help us to improve our proof by finding hidden lemmas. And proofs help us improve our conjecture by finding conditions on its validity. Either way, or both ways, mathematical knowledge grows. And as it grows, its concepts are refined. We begin with a vague, unarticulated notion of what a polyhedron is. We have a conjecture about polyhedra and an informal proof of it. Counterexamples or refutations “stretch” our original concept: is a picture frame a genuine polyhedron, or a cylinder, or two polyhedra joined along a single edge?
Attempts to rescue our conjecture from refutation yield “proof-generated definitions” like that of a “normal polyhedron”.
Is there any limit to this process of “concept-stretching”, or any distinction to be drawn between interesting and frivolous concept-stretching? Can this process yield, not fallible conjectures and proofs, but certainty? Lakatos’s editors distinguish the certainty of proofs from the certainty of the axioms from which all proofs must proceed. They claim that rigorous proof-procedures have been attained, and that “There is no serious sense in which such proofs are fallible” (P&R: 57). Quite so. But only because we have decided not to “stretch” the logical concepts that lie behind those rigorous and formalizable proof-procedures. A rigorous proof in classical logic may not be valid in intuitionistic or paraconsistent logics. And the key point is that a proof, however rigorous, only establishes that if the axioms are true, then so is the theorem. If the axioms themselves remain fallible, then so do the theorems rigorously derived from them. Providing foundations for mathematics requires the axioms to be made certain, by deriving them from logic or set theory or something else. Lakatos claimed that this foundational project had collapsed (see below, §3.2).
To what extent is this imaginary dialogue a contribution to the history of mathematics? Lakatos explained that
The dialogue form should reflect the dialectic of the story: it is meant to contain a sort of rationally reconstructed or “distilled” history. The real history will chime in in the footnotes, most of which are to be taken, therefore, as an organic part of the essay (P&R: 5).
This device, first necessitated by the dialogue form, became a pervasive theme of Lakatos’s writings. It was to attract much criticism, most of it centred around the question whether rationally reconstructed history was real history at all. The trouble is that the rational and the real can come apart quite radically. At one point in Proofs and Refutations a character in the dialogue makes a historical claim which, according to the relevant footnote, is false. Lakatos says that the statement
although heuristically correct (i.e. true in a rational history of mathematics) is historically false. This should not worry us: actual history is frequently a caricature of its rational reconstructions. (P&R: 21)
On occasions, Lakatos’s sense of humour ran away with him, as when the text contains a made-up quotation from Galileo, and the footnote says that he “was unable to trace this quotation” (P&R: 62). (Though this does rather smack of his youthful habit of winning arguments with “bourgeois” students by fabricating on-the-spot quotations from the authorities they respected. See Bandy 2009: 122.) Horrified critics protested that rationally reconstructed history is a caricature of real history, not in fact real history at all but rather “philosophy fabricating examples”. One critic said that philosophers of science should not be allowed to write history of science. This academic trade unionism is misguided. You do not falsify history by pointing out that what ought to have happened did not, in fact, happen.
There is an important pedagogic point to all this, too. The dialectic of proofs and refutations can generate, in the ways explained above, quite complicated definitions of mathematical concepts, definitions that can only really be understood by considering the process that gave rise to them. But mathematics teaching is not historical, or even quasi-historical. (One sense in which Lakatos’s theory is dialectical: it represents a process as rational even though the terms of the debate are not clearly defined.) But students nowadays are presented with the latest definitions at the outset, and required to learn them and apply them, without ever really understanding them.
One question about Proofs and Refutations is whether the heuristic patterns depicted in it apply to the whole of mathematics. While some aspects clearly are peculiar to the particular case-study of polyhedra, the general patterns are not. Lakatos himself applied them in a second case-study, taken from the history of analysis in the nineteenth century (“Cauchy and the Continuum”, 1978c).
3.2 “Regress” and “Renaissance”
The onslaught on formalism continues in a pair of papers “Infinite Regress and the Foundations of Mathematics” (1962) and “A Renaissance of Empiricism in the Recent Philosophy of Mathematics?” (1967a). Here Popper predominates and Hegel recedes. Regress is a critique of both logicism and formalism proper (that is, Hilbert’s programme), concentrating primarily on Russell. Russell sought to rescue mathematics from doubt and uncertainty by deriving the totality of mathematics from self-evident logical axioms via stipulative definitions and water-tight rules of inference. But the discovery of Russell’s Paradox and the felt need to deal with the Liar and related paradoxes blew this ambition sky-high. For some of the axioms that Russell was forced to posit—the Theory of Types which Lakatos sees, in effect, as a monster-barring definition (elevated into an axiom) that avoids the paradoxes by excluding self-referential propositions as meaningless; the Axiom of Reducibility which is needed to relax the unduly restrictive Theory of Types; the Axiom of Infinity which posits an infinity of objects in order to ensure that every natural number has a successor; and the Axiom of Choice (which Russell refers to as the multiplicative axiom)—were either not self-evident, not logical or both. Russell’s fall-back position was to argue that mathematics was not justified by being derivable from his axioms but that his axioms were justified because the truths of mathematics could be derived from them whilst avoiding contradictions:
When pure mathematics is organized as a deductive system…it becomes obvious that, if we are to believe in the truth of pure mathematics, it cannot be solely because we believe in the truth of the set of premises. Some of the premises are much less obvious than some of their consequences, and are believed chiefly because of their consequences. (Russell 2010 [1918]: 129)
As Lakatos amply documents in Renaissance, a surprising number of labourers in the foundationalist vinyard—Carnap and Quine, Fraenkel and Gödel, Mostowski and von Neumann—were prepared to make similar noises. Lakatos dubs this development “empiricism” (or “quasi-empiricism”) and hails it on the one hand whilst condemning it on the other.
Why “empiricism”? Not because it revives Mill’s idea that the truths of arithmetic are empirical generalizations, but because it ascribes to mathematics the same kind of hypothetico-deductive structure that the empirical sciences supposedly display, with axioms playing the part of theories and their mathematical consequences playing the part of observation-statements (or in Lakatos’s terminology, “potential falsifiers”).
Why does Lakatos hail the “empiricism” that he also condemns? Because it means that mathematics has the same kind epistemic structure that science has according to Popper. It’s a matter of axiomatic conjectures that can be mathematically refuted. (The difference between science and mathematics consists in the differences between the potential falsifiers.)
Why does Lakatos condemn the “empiricism” that he also commends? Because Russell, like most of his supporters, succumbs to the “inductivist” illusion that the axioms can be confirmed by the truth of their consequences. In Lakatos’s opinion this is simply a mistake. Truth can trickle down from the axioms to their consequences and falsity can flow upwards from the consequences to the axioms (or at least to the axiom set). But neither truth nor probability nor justified belief can flow up from the consequences to the axioms from which they follow. Here Lakatos out-Poppers Popper, portraying not just science but even mathematics as a collection of unsupported conjectures that can be refuted but not confirmed, anything else being condemned as to “inductivism”. However the inductivism that Lakatos scornfully rejects in Renaissance is just the kind of inductivism that he would be recommending to Popper just a few years later.
3.3 “Changes in the Problem of Inductive Logic” (1968)
In 1964 Lakatos turned from the history and philosophy of mathematics to the history and philosophy of the empirical sciences. He organised a famous International Colloquium in the Philosophy of Science, held in London in 1965. Participants included Tarski, Quine, Carnap, Kuhn, and Popper. The Proceedings ran to four volumes (Lakatos (ed.) 1967 & 1968, and Lakatos and Musgrave (eds.) 1968 & 1970). Lakatos himself contributed three major papers to these proceedings. The first of these (Renaissance) has been dealt with already. The second, “Changes in the Problem of Inductive Logic” (Changes), analyses the debate between Carnap and Popper regarding the relations between theory and evidence in science. It is remarkable both for its conclusions and for its methodology. The conclusion, to put it bluntly, is that a certain brand of inductivism is bunk. The prospects for an inductive logic that allows you to derive scientific theories from sets of observation statements, thus providing them with a weak or probabilistic justification, are dim indeed. There is no inductive logic according to which real-life scientific theories can be inferred, “partially proved” or “confirmed (by facts) to a certain degree”’ (Changes: 133). But Lakatos sought to prove his point by analysing the Popper/Carnap debate and reversing the common verdict that Carnap had won and that Popper had lost. And here he faced a problem. As Fox (1981) explains:
The facts on which the verdict was based were that Popper’s claimed refutations of Carnap all failed, through either fallacy or misrepresentation, and that Carnap was a careful, precise, irenic thinker, in the habit of stating as his conclusions exactly what his premises warranted. The standards on which the verdict was based were the respectable professional ones by which we mark third-year essays. The verdict was: Carnap gets an A+, and Popper’s refusal to wither away is a moral and intellectual embarrassment. (Fox 1981: 94.)
Lakatos’s strategy was to accept the facts but reverse the value-judgment by developing the twin concepts of a degenerating research programme and a degenerating problem-shift and applying them to Carnap’s successive endeavours. But Carnap’s programme was philosophico-mathematical rather than scientific. So what was wrong with it could not be that it failed to predict novel facts or that its predictions were mostly falsified. For it was not in the business of predicting empirical observations whether novel or otherwise. (Indeed Lakatos’s concept of a degenerating philosophical programme seems to have preceded his concept of a degenerating scientific programme.) So what was wrong with Carnap’s enterprise? In an effort to solve his original problem, Carnap had to solve a series of sub-problems. Some were solved, others were not, generating sub-sub-problems of their own. Some of these were solved, others were not, generating sub-sub-sub-problems and sub-sub-sub-sub-problems etc. Since some of these sub-problems (or sub-sub-problems) were solved, the programme appeared to its proponents be busy and progressive. But it was drifting further and further away from achieving its original objectives.
Now for Lakatos, such problem-shifts are not necessarily degenerating. If a programme ends up solving a problem that it did not set out to solve, that is all fine and dandy so long as the problem that it succeeds in solving is more interesting and important than the problem that it did set out to solve.
But one may solve problems less interesting than the original one; indeed, in extreme cases, one may end up solving (or trying to solve) no other problems but those which one has oneself created while trying to solve the original problem. In such cases we may talk about a degenerating problem-shift. (Changes: 128–9.)
Thus Carnap starts off with the exciting problem of showing how scientific theories can be partially confirmed by empirical facts and ends up with technical papers about drawing different coloured balls out of an urn. In Lakatos’s opinion this does not constitute intellectual progress. Carnap had lost the plot.
3.4 “Falsification and the Methodology of Scientific Research Programmes” (1970)
The best-known of Lakatos’s “Conference Proceedings” is Criticism and the Growth of Knowledge, which became an international best-seller. It contains Lakatos’s important paper “Falsification and the Methodology of Scientific Research Programmes” (FMSRP) which we have discussed already. A briefer account of this methodology had already appeared (Lakatos 1968a), in which Lakatos distinguished dogmatic, naïve and sophisticated falsificationist positions, attributing them to “Popper0, Popper1 and Popper2”—or as he otherwise put it, “proto-Popper, pseudo-Popper and proper-Popper”. (Popper did not appreciate being disassembled into temporal or ideological parts and protested “I am not a Trinity”.)
Lakatos’s methodology has been seen, rightly, as an attempt to reconcile Popper’s falsificationism with the views of Thomas Kuhn. Popper saw science as consisting of bold explanatory conjectures, and dramatic refutations that led to new conjectures. Kuhn (and Polanyi before him) objected that
No process yet disclosed by the historical study of scientific development at all resembles the methodological stereotype of falsification by direct comparison with nature (Kuhn 1962: 77).
Instead, science consists of long periods of “normal science”, paradigm-based research, where the task is to force nature to fit the paradigm. When nature refuses to comply, this is not seen as a refutation, but rather as an anomaly. It casts doubt, not on the ruling paradigm, but on the ingenuity of the scientists—“only the practitioner is blamed, not his tools”. It is only in extraordinary periods of “revolutionary science” that anything like Popperian refutations occur.
Lakatos proposed a middle-way, in which Kuhn’s socio-psychological tools were replaced by logico-methodological ones. The basic unit of appraisal is not the isolated testable theory, but rather the “research programme” within which a series of testable theories is generated. Each theory produced within a research programme contains the same common or “hard core” assumptions, surrounded by a “protective belt” of auxiliary hypotheses. When a particular theory is refuted, adherents of a programme do not pin the blame on their hard-core assumptions, which they render “irrefutable by fiat”. Instead, criticism is directed at the hypotheses in the “protective belt” and they are modified to deal with the problem. Importantly, these modifications are not random—they are in the best cases guided by the heuristic principles implicit in the “hard core” of the programme. A programme progresses theoretically if the new theory solves the anomaly faced by the old and is independently testable, making new predictions. A programme progresses empirically if at least one of these new predictions is confirmed.
Notice that a programme can make progress, both theoretically and empirically, even though every theory produced within it is refuted. A programme degenerates if its successive theories are not theoretically progressive (because it predicts no novel facts), or not empirically progressive (because novel predictions get refuted). Furthermore, and contrary to Kuhn’s idea that normally science is dominated by a single paradigm, Lakatos claimed that the history of science typically consists of competing research programmes. A scientific revolution occurs when a degenerating programme is superseded by a progressive one. It acquires hegemonic status though its rivals may persist as minority reports.
Kuhn saw all this as vindicating his own view, albeit with different terminology (Kuhn 1970: 256, 1977: 1). But this missed the significance of replacing Kuhn’s socio-psychological descriptions with logico-methodological ones. It also missed Lakatos’s claim that there are always competing programmes or paradigms. Hegemony is seldom as total as Kuhn seems to suggest.
3.5 “The History of Science and Its Rational Reconstructions” (1971)
As we have seen, in Proofs and Refutations Lakatos had already joked that “actual history is frequently a caricature of its rational reconstructions”. The use of the plural—“reconstructions”—is important. There is more than one way of rationally reconstructing history, and how you do it depends upon what you count as rational and what not—it depends, in short, in your theory of rationality. There is not one “rational history”—as Hegel may have thought—but several competing ones. And, in a remarkable dialectical turn, Lakatos proposed that one can evaluate competing theories of rationality by asking how well they enable one to reconstruct the history of science (whether it be mathematics or empirical science). The thought is that if your philosophy of science, or theory of scientific rationality, deems most of “great science” irrational, then something is wrong with it. Contrariwise, the more of the history of “great science” your theory of rationality deems rational, the better that theory is.
The obvious worry is that this meta-criterion for theories of scientific rationality threatens to deprive the philosophy of science of any critical bite. Will not the best philosophy of science simply say that whatever scientists do is rational, that scientific might is right, that the best methodology is Feyerabend’s “Anything goes”? Lakatos’s Kantian epigram “Philosophy of science without history of science is empty; history of science without philosophy of science is blind” threatens to eliminate the philosophy of science altogether, in favour of historical-sociological studies of the decisions of scientific communities. (One of us discusses this problem, and attempts to disarm the worry, in Musgrave 1983.)
Another worry, which is perhaps less obvious, is that Lakatos seems to be implicitly appealing to the kind of inductive principle that he scorns elsewhere. Isn’t he saying that a sequence of successes in the history of science displaying key episodes as rational tends to confirm a theory of scientific rationality?
Lakatos himself was a master of philosophically inspired case-studies of episodes in the history of science—Feyerabend said he had turned this into an art form. His “Hegelian” idea that the “rationally reconstructed” history of thought has primacy is emphasised in two books, Larvor 1998 and Kadvany 2001. After his death, a Colloquium was held in Nafplion, Greece, where case-studies applying Lakatos’s ideas to episodes from the history of both the natural and social sciences were presented by his students and colleagues. The Proceedings of this “Nafplion Colloquium” were subsequently published in two volumes—Howson (ed.) 1976 and Latsis (ed.) 1976. Further case-studies include Zahar 1973 and Urbach 1974.
However, Urbach’s paper, which was written with Lakatos’s active collaboration and encouragement (F&AM: 348–34), represents something of an “own goal” for the MSRP. Urbach argued that the environmentalist programme in IQ Studies, which tries to explain intergroup differences in tested intelligence as due to environmental causes, was a degenerating research programme. At least it was degenerating when compared to its hereditarian rival which puts these differences down to differences in hereditary endowments. The tables were dramatically turned just thirteen years later with the discovery of the Flynn effect (1987) which showed massive differences in intergroup IQs which simply could not be explained by hereditary differences. (The groups in question were genetically identical, the higher scoring groups being the children or the grandchildren of the lower scoring groups. See Flynn 1987 and 2009.) Thus the supposedly “degenerate” programme was propelled into the lead. Of course the MSRP allows for such dramatic reversals of fortune, but it is at least a bit embarrassing if a programme damned as degenerate by both the Master and one of his chief disciples is spectacularly vindicated just thirteen years later.
3.6 “Popper on Demarcation and Induction” (1974)
“Popper on demarcation and induction” (PDI) was written in 1970 for the Popper volume in the Library of Living Philosophers series (Schilpp (ed.) 1974). Sadly, it caused a major falling out with Popper despite the generous praise in its opening sections:
Popper’s ideas represent the most important development in the philosophy of the twentieth century; an achievement in the tradition—and on the level—of Hume, Kant, or Whewell. … More than anyone else, he changed my life. I was nearly forty when I got into the magnetic field of his intellect. His philosophy helped me to make a final break with the Hegelian outlook which I had held for nearly twenty years. (PDI: 139.)
Much of the paper is devoted to criticizing Popper’s demarcation criterion and arguing for his own. Most of these criticisms have been canvased already. Lakatos argues, for instance, that Popper’s falsificationism can be falsified
by showing that the best scientific achievements were unscientific [by Popper’s standards] and that the best scientists, in their greatest moments, broke the rules of Popper’s game of science (PDI: 146).
But Lakatos also develops a criticism that has nothing much to do with the differences between his demarcation criterion and Popper’s, indeed a criticism that seems equally telling against Popper’s philosophy and his own.
Lakatos points out that when Popper first wrote his classic Logik der Forschung (LSD) in the early 1930s, the correspondence theory of truth was regarded with deep suspicion by the empiricist philosophers that he was trying to convince. Accordingly Popper was careful to state that
in the logic of science here outlined it is possible to avoid using the concepts “true” and “false” … We need not say that the theory is “false” [or “falsified”], but we may say instead that it is contradicted by a certain set of accepted basic statements. Nor need we say of basic statements that they are “true” or “false”, for we may interpret their acceptance as the result of a conventional decision, and the accepted statements as results of this decision. (LSD: 273–274.)
But shortly thereafter Popper met Tarski who convinced him that the correspondence theory of truth was philosophically respectable, and this liberated him to declare that truth, or truth-likeness was the object of the scientific enterprise (LSD: 273n). Lakatos apparently endorses this development.
Tarski’s rehabilitation of the correspondence theory of truth…stimulated Popper to complement his logic of discovery with his own theory of verisimilitude and of approximation to the Truth, an achievement marvellous both in its simplicity and in its problem-solving power. (PDI: 154.)
But Lakatos points out a problem. There is now a disconnect between the game of science and the aim of science. The game of science consists in putting forward falsifiable, risky and problem-solving conjectures and sticking with the unrefuted and the well-corroborated ones. But the aim of science consists in developing true or truth-like theories about a largely mind-independent world. And Popper has given us no reason to suppose that by playing the game we are likely to achieve the aim. After all, a theory can be falsifiable, unfalsified, problem-solving and well-corroborated without being true.
To restore the connection between the game and its aim Lakatos makes a plea with Popper for a “whiff of ‘inductivism’” (PDI: 159). What is this whiff?
An inductive principle which connects realist metaphysics with methodological appraisals, verisimilitude with corroboration, which reinterprets the rules of the “scientific game” as a—conjectural—theory about the signs of the growth of knowledge, that is, about the signs of growing verisimilitude of our scientific theories (PDI: 156).
In other words, it is a metaphysical principle which states that highly falsifiable but well-corroborated theories are (in some sense) more likely to be true (or truth-like) than their low-risk counterparts. Corroborations tend to confirm. Thus by playing the game we approximate the aim. Lakatos goes on to urge that this whiff of inductivism is not much of an ask, since Popper sometimes seems to presuppose it without fully realizing that he is doing so.
There are three points to note.
(1) If this criticism holds good against Popper it is equally good against Lakatos himself. He too has a disconnect between the game of science—which, when it is played well, consists in developing progressive research programmes—and the aim of science—which, like Popper, he takes to be truth (FMSRP: 58). To solve this problem, we need a metaphysical principle which states that highly progressive research programmes are (in some sense) more likely to be true (or truth-like) than their degenerating rivals. Thus if Popper could do with a whiff of inductivism, the same goes for Lakatos.
(2) The inductivism that Lakatos recommends to Popper looks remarkably like the inductivism that he condemned in Russell. (“I do not see any way out of a dogmatic assertion that we know the inductive principle, or some equivalent; the only alternative is to throw over almost everything that is regarded as knowledge by science and common sense.” Russell 1944: 683, quoted disdainfully by Lakatos at Regress: 18.) But if inductivism is permissible (or even de rigueur) in the Philosophy of Science, perhaps it is permissible (or even de rigueur) in the Philosophy of Mathematics! In which case, the Renaissance of Empiricism in the Philosophy of Mathematics may count as a genuine renaissance after all, since the logical or set-theoretic axioms may (as Russell supposed) be confirmed (and hence rationally believed) because of their mathematical consequences. If epistemic support can flow upwards from evidence to theory (where the evidence consists of a sequence of novel and successful predictions), perhaps it can flow upwards from consequences to axioms.
(3) This episode undermines an influential “Hegelian” reading of Lakatos due to Ian Hacking. According to Hacking,
Lakatos, educated in Hungary in an Hegelian and Marxist tradition, took for granted the post-Kantian, Hegelian, demolition of correspondence theories (Hacking 1983: 118).
This is an odd assertion as Lakatos explicitly endorses the correspondence theory on a number of occasions and even declares truth to be the aim of science, which is why contradictions are intolerable in the long term (FMSRP: 58). But in Hacking’s view, Lakatos was
down on truth, not just a particular theory of truth. He [did] not want a replacement for the correspondence theory, but a replacement for truth itself (Hacking 1983: 119).
He found his replacement in the concept of progress.
Lakatos then defines objectivity and rationality in terms of progressive research programmes, and allows an incident in the history of science to be objective and rational if its internal history can be written as a sequence of progressive problem shifts (Hacking 1983: 126).
Progress becomes a surrogate for truth. We don’t ask whether a theory is true or not but only whether it is part of a progressive programme. To paraphrase the young Karl Popper,
in the logic of science [that Lakatos has] outlined it is possible to avoid using the concepts “true” and “false” [which, in Lakatos’s opinion, is a jolly good thing!] (LSD: 273).
But if Lakatos had really been such an anti-truth-freak, he would not have congratulated Popper on his Tarskian turn. Rather he would have condemned him for taking the vacuous concept of truth to be the aim of science. As for the disconnect between the aim of science and the game of science, he would have recommended that Popper resolve it by dropping the aim and substituting the game (which, according to Hacking, was what Lakatos himself was trying to do). If truth were not the object of the exercise, there would be no need for a whiff of inductivism to connect Popper’s method with science’s ultimate objective. But Lakatos did think that a whiff of inductivism was needed to connect Popper’s method with science’s objective. Hence Lakatos believed that truth was the object of the scientific enterprise. Whatever the remnants of Hegelianism that Lakatos retained in later life, an aversion to truth (or to the correspondence theory of truth ) was not one of them.
3.7 “Why Did Copernicus’s Research Programme Supersede Ptolemy’s?” (1976)
Lakatos’s last publication was an historical a case-study, co-authored with Elie Zahar and published after his death. It argues that the methodology of scientific research programmes can explain the Copernican Revolution as a rational process by which an earlier theory (Ptolemy’s geocentric theory of the Cosmos) was dethroned in favour another objectively better one (Copernicus’s heliocentric theory). It thus demonstrates the rationality of the Copernican Revolution (one of the most dramatic episodes in the history of thought) and confirms the MSRP as a theory of scientific rationality (so long as we accept the inductive principle that the more “great science” that a demarcation criterion can represent as rational, the more likely it is to be correct).
Apart from the intrinsic interest of the subject, the paper marks a modification of Lakatos’s conception of factual novelty and hence a modification to the MSRP. For the earlier Lakatos, a fact counts as novel with respect to a research programme if it is not predicted by any of its rivals and if it is not already known. In WDCRPSP Lakatos accepts an amendment due to his co-author Elie Zahar. Zahar’s original problem was our old friend the Precession of Mercury. This was explained by Einstein’s programme—specifically the General Theory of Relativity—but not by Newton’s, and this was generally thought to count in Einstein’s favour. The difficulty is that in Lakatos’s lexicon the Precession of Mercury did not count as a novel fact. After all it had been known to astronomers for nearly a century. Thus, given the original version of the MSRP, the discovery that that the General Theory could explain the Precession of Mercury (whilst Newton’s theory could not) did not mean that Einstein’s programme was any more progressive than Newton’s. (That had to be argued on other grounds.) But this is such a counterintuitive result that it suggests a defect in the MSRP. Zahar’s modification is that a fact counts as a novel prediction with respect to a research programme if a) it is not predicted by any of the programme’s rivals and b) either it is not already known or if it is already known, the hard core of the programme was not devised to explain it.
By this modified criterion the Precession of Mercury counts as a novel fact with respect to Einstein’s programme. For the General Theory was designed to solve a different set of problems. The prediction that if the General Theory were correct, the perihelion of Mercury would shift as it does without the influence of any other heavenly body came as an “unexpected present from Schwarzschild” (the man who did the sums). It was therefore “an unintended by-product of Einstein”s programme’ (WDCRPSP: 185). So despite its antiquity, the Precession of Mercury counts as a novel fact or a novel prediction with respect to Einstein’s programme, thus making the programme a lot more progressive. Some might regard Zahar’s amendment as a suspiciously ad hoc move, but ad hoc or not, it looks like an improvement on the original MSRP. Lakatos and Zahar go on to use this idea to explain why Copernicus’s programme very properly superseded Ptolemy’s.
4. Mincemeat Unmade: Lakatos versus Feyerabend
According to his friend Paul Feyerabend, Lakatos was “was a fascinating person, an outstanding thinker and the best philosopher of science of our strange and uncomfortable century” (Feyerabend 1975a: 1). Writing in 1981, John Fox raised a cynical eyebrow:
As when Lakatos similarly praises Popper, it is easy to suspect indirect self-advertisement: building up one’s opponent so that the announced victory is taken as winning a world title (Fox 1981: 92).
With Motterlini’s publication of the Feyerabend/Lakatos correspondence (F&AM), Fox’s suspicions have been amply confirmed. It is quite clear that Lakatos and Feyerabend were engaged in a self-conscious campaign of mutual boosterism, leading up to a planned epic encounter between a fallibilistic rationalism, as represented by Lakatos, and epistemological anarchism, as represented by Feyerabend. As Feyerabend put it “I was to attack the rationalist position, Imre was to restate and defend it, making mincemeat of me in the process” (Feyerabend 1975b: preface). This Battle of the Titans was to consist of Feyerabend’s Against Method and Lakatos’s projected reply, which is referred to, in their correspondence, by the mysterious acronym “MAM”.
Sometimes the mutual boosterism went a bit too far, causing pain and distress to serious-minded philosophers who regarded Popperian critical rationalism as a bulwark against a resurgent Nazism:
Hans Albert is on the verge of suicide [writes Lakatos to Feyerabend]. Allegedly somebody told him that in Kiel you will describe critical rationalism as a “mental disease”, and he thinks that will be the end of Reason in Germany. I told him that though you are AN EXTREMELY GREAT MAN, that you will not bring Nazism back single-handedly…. (F&AM: 291).
But although they had interested motives for talking each other up, it is clear that the mutual admiration between Feyerabend and Lakatos was quite sincere. Each genuinely regarded the other as the man to beat.
Feyerabend’s criticism of Lakatos is summed up in his joking dedication to Against Method: To IMRE LAKATOS Friend and Fellow-Anarchist. In other words Feyerabend’s charge is that for all his law-and-order pretensions as a defender of the rationality of science and a critic of pseudoscience, Lakatos is really an epistemic anarchist malgré lui. Feyerabend’s epistemological anarchism is sometimes summed up by the slogan “Anything goes” but that is a little misleading. His point is rather this: If you want a set of methodological rules distinguishing between good science and bad science, the only thing that won’t exclude some of what you (Dear Reader) regard as the best science is the principle “Anything goes”. Anything else would rule out what is widely regarded as some of the best science as unscientific. Thus a large proportion of Feyerabend’s Against Method is devoted to “praising” Galileo for his allegedly anti-Popperian practices and his dodgy (but progressive) rhetorical tricks. Everyone agrees that Galileo was a great scientist. But if Galileo was great, then the rules that supposedly constitute great science are defective since they would exclude some of the greatest of Galileo’s great deeds.
But what about Lakatos? Feyerabend poses a dilemma. Suppose we apply the Lakatos’s methodology of scientific research programmes in a conservative or rigouristic spirit. Scientists are urged to abandon degenerating research programmes in favour of the progressive, and grant-giving agencies are urged to defund them. After all, such programmes are condemned by the Demarcation Criterion as bad science or even non-science! At the very least, the adherents of degenerating research programmes must bear the stigma of irrationality, owning up to their scientific sins. But in that case Lakatos’s MSRP would be condemning some research programmes to death as bad science or even non-science that might otherwise recover their progressive (and hence their scientific) status. Thus Lakatos would be vulnerable to the same criticism that he himself applies to Popper—he would be excluding some of the best science as unscientific (that is, research programmes that have suffered a degenerating phase only to stage a magnificent comeback). In response to this, Lakatos distinguished appraisal from advice, and said that the task of the philosopher of science is to issue rules of appraisal, not to advise scientists (or grant-giving agencies) about what they ought to do. The Demarcation Criterion can evaluate the current state of play but it does not tell anyone what to do about it. (To paraphrase Marx’s Thesis XI, “Methodologists hitherto have attempted to change the world of scientific research in various ways; the point, however is to appraise it”.) The MSRP does enjoin a principle of scientific honesty, namely that the adherents of degenerating research programmes should own up to their methodological shortcomings, such as the lack of novel predictions or the falsification of the predictions that they have made. However, so long as they admit to these failures they can (rationally?) persist in their degenerate ways.
But in that case Lakatos is gored by the other horn of Feyerabend’s dilemma. For Feyerabend argues that a Demarcation Criterion that cannot tell anyone what to do or not to do is scarcely distinguishable from “Anything goes”. To revert to Feyerabend’s political analogy, what is the difference between an anarchist society and a “state” where the “police” can appraise people for their “criminal” or “law-abiding” behaviour but can never make an arrest or send anyone to jail? That’s a “state” which isn’t a state and a “police force” which isn’t a police force! We have not scientific law-and-order but anarchy, accompanied by uplifting sermons and benedictions posthumously bestowed on the mighty scientific dead.
What was Lakatos’s response to this dilemma? It is sometimes suggested, not least by Feyerabend himself, that Lakatos did have, or would have had, an answer but that he did not live to write it up. Their correspondence suggests otherwise. Although the locus classicus of Feyerabend’s argument is chapter 16 of Against Method (1975b) he had already developed his dilemma in “Consolations for the Specialist” (1968) and Lakatos had access to successive versions of the argument in the successive drafts that Feyerebend sent him in the last is six years of his life. Yet there is no trace of a counterargument in Lakatos’s surviving letters to Feyerabend. Instead there are a series of fearsome threats.
I am now greatly grateful for your depicting me as God and yourself as the Devil. I also return the compliment: for me you are the only philosopher worth demolishing. But there is one trouble: I can take you to such little pieces that only an electromicroscope can discover you again. Will you be very hurt? (F&AM: 268–9.)
However, aside from these threats, a developed answer to Feyerabend’s dilemma is conspicuous by its absence. One is reminded of King Lear:
I will do such things,—
What they are, yet I know not: but they shall be
The terrors of the earth.
The upshot is that if there is a Lakatosian answer to Feyerabend’s dilemma, it is an answer that has to be concocted on his behalf. One of us has a go in Musgrave 1976, but for the Methodology of Scientific Research Programmes, it is still, very much, an open problem.
Bibliography
Works by Lakatos
- 1946a: “Citoyen és Munkásosztály” (Citoyen and the working class), Valóság, 1: 77–88.
- 1946b: “A fizikai Idealizmus Bírálata” (A critique of idealism in physics); a review of Susan Stebbing’s Philosophy and the Physicists, Athenaeum, 1: 28–33.
- 1947a: “Huszadik Század”, Forum, 1: 316–20.
- 1947b: “Eötvös Collégium—Györffy Kollégium”, Valóság, 2: 107–24.
- 1947c: “Jeges Károly: Megtanulom a fizikát”, Társadalmi Szemle, 1: 472.
- 1947d: “Természettudományos világnézet és demokratikus nevelés” (Scientific worldview and democratic upbringing), Embernevelés, 2: 63–66.
- 1947e: “Modern fizika—modern társadalom” (Modern physics—modern society), in Kemény Gábor (ed.), Továbbképzés és demokrácia. [There is an English translation of this essay in Kampis et al. 2002: 356–368.]
- 1947f: “‘Haladó tudós’ a demokráciában” (A “progressive scholar” in a democracy), Tovább, June 13.
- 1956: Speech at the Pedagogy Debate of the Petőfi Circle on September 28, 1956; transcript published in András B. Hegedűs (ed.), A Petőfi Kör vitái (The debates of the Petőfi Circle), Vol. VI, Budapest: Intézet and Múzsák Kiadó, 1992, 34–38. [English translation “On rearing scholars” in Motterlini 1999: 375–381.]
- 1961: “Essays in the Logic of Mathematical Discovery”. Unpublished PhD dissertation, Cambridge University.
- 1962 [Regress]: “Infinite Regress and Foundations of Mathematics”, Aristotelian Society Supplementary Volume, 36: 155–94. [Republished as chapter 1 of Lakatos 1978b (PP2), cited pages from this version.]
- 1963: Discussion of “History of Science as an Academic Discipline” by A.C. Crombie and M.A. Hoskin, in A.C. Crombie (ed.), Scientific Change, London: Heinemann, pp. 781–5. [Republished as chapter 13 of Lakatos 1978b (PP2).]
- 1963–4: “Proofs and Refutations”, in the British Journal for the Philosophy of Science, 14: 1–25, 120–139, 221–243, 296–342. [Reprinted in Lakatos 1976c (P&R). cited pages from this version.]
- 1967a [Renaissance]: “A Renaissance of Empiricism in the Recent Philosophy of Mathematics”, in Lakatos 1967b: 199–202. [Republished in an expanded form as 1978b (PP2), cited pages from this version.]
- 1967b: (ed.), Problems in the Philosophy of Mathematics, Amsterdam: North-Holland.
- 1968a: “Criticism and the Methodology of Scientific Research Programmes”, Proceedings of the Aristotelian Society, 69: 149–186.
- 1968b [Changes]: “Changes in the Problem of Inductive Logic”, in Lakatos 1968c, 315–417 [Reprinted as chapter 8 of PP2, cited pages from this version.]
- 1968c: (ed.), The Problem of Inductive Logic, Amsterdam: North-Holland.
- 1968d: (edited with A. Musgrave) Problems in the Philosophy of Science, Amsterdam: North-Holland.
- 1968e: “A Letter to the Director of the London School of Economics”, in C.B. Cox and A.E. Dyson (eds.), Fight for Education, A Black Paper, London: Critical Quarterly Society, 28–31. [Republished as chapter 12 of Lakatos 1978b (PP2), referred to, in this reprint, as LTD.]
- 1970a [FMSRP]: “Falsification and the Methodology of Scientific Research Programmes”, in Lakatos 1970b, 91–196 (Republished as chapter 1 of Lakatos 1978a, PP1, cited pages from this version.)
- 1970b, editor with A. Musgrave: Criticism and the Growth of Knowledge, Cambridge: Cambridge University Press.
- 1970c: Discussion of “Knowledge and Physical Reality” by A. Mercier, in A.D. Breck and W. Yourgrau (eds.), Physics, Logic and History, New York: Plenum Press, pp. 53–4.
- 1970d: Discussion of ‘Scepticism and the Study of History’ by Richard H. Popkin, in A.D. Breck and W. Yourgrau (eds.), Physics, Logic and History, New York: Plenum Press, pp. 220–3.
- 1971a [HS&IRR]: “The History of Science and its Rational Reconstructions”, in R.C. Buck and R.S. Cohen (eds.), PSA 1970: Boston Studies in the Philosophy of Science, 8, Dordrecht: Reidel, pp. 91–135. [Republished as chapter 2 of Lakatos 1978a (PP1), cited pages from this version]
- 1971b: “Replies to Critics”, in R.C. Buck and R.S. Cohen (eds.): PSA 1970: Boston Studies in the Philosophy of Science, 8, Dordrecht: Reidel, pp. 174–82.
- 1974a: “Discussion Remarks on Papers by Ne‘eman, Yahil, Beckler, Sambursky, Elkana, Agassi, Mendelsohn”, in Y. Elkana (ed.), The Interaction Between Science and Philosophy, Atlantic Highlands, New Jersey: Humanities Press, pp. 41, 155–6, 163, 165, 167, 280–3, 285–6, 288–9, 292, 294–6, 427–8, 430–1, 435.
- 1974b [PDI]: “Popper on Demarcation and Induction”, in P.A. Schilpp (ed.), The Philosophy of Karl Popper, La Salle: Open Court, 241–73. [Republished as chapter 3 of Lakatos 1978a (PP1), cited pages from this version.]
- 1974c: “The Role of Crucial Experiments in Science”, Studies in the History and Philosophy of Science, 4: 309–25.
- 1974d [S&P]: “Science and Pseudoscience”, in Vesey, G. (ed.), Philosophy in the Open, Open University Press. [Republished as the introduction to Lakatos1978a (PP1), cited pages from this version.]
- 1976a: [UT] “Understanding Toulmin”, Minerva, 14: 126–43. [Republished as chapter 11 of Lakatos 1978b.]
- 1976b [Renaissance]: “A Renaissance of Empiricism in the Recent Philosophy of Mathematics?”, British Journal for the Philosophy of Science, 27: 201–23. [Republished as chapter 2 of Lakatos 1978b (PP2), cited pages from this version.]
- 1976c [P&R]: Proofs and Refutations: The Logic of Mathematical Discovery, J. Worrall and E. Zahar (eds.), Cambridge: Cambridge University Press
- 1976d [WDCRPSP]: “Why Did Copernicus’s Programme Supersede Ptolemy’s?”, by I. Lakatos and E.G. Zahar, in R. Westman (ed.), The Copernican Achievement, Los Angeles: University of California Press, 354–83. [Republished as chapter 5 of PP1, cited pages from this version.]
- 1978a [PP1]: The Methodology of Scientific Research Programmes (Philosophical Papers: Volume 1), J. Worrall and G. Currie (eds.), Cambridge: Cambridge University Press.
- 1978b [PP2]: Mathematics, Science and Epistemology (Philosophical Papers: Volume 2), J. Worrall and G. Currie (eds.), Cambridge: Cambridge University Press.
- 1978c: “Cauchy and the Continuum:the Significance of Non-Standard Analysis for the History and Philosophy of Mathematics”. [Published as chapter 5 of PP1]
- 1999a: “Lectures on Scientific Method” in Motterlini 1999: 19–109
- 1999b: “Lakatos-Feyerabend Correspondence” in Motterlini 1999: 119–374.
- 1999c: “On Rearing Scholars” in Motterlini 1999: 375–381.
- 1999d: “The Intellectuals’ Betrayal of Reason” in Motterlini 1999: 393–397.
Secondary Literature
- Ariew, R., 2014, “Pierre Duhem”, The Stanford Encyclopedia of Philosophy (Fall 2014 edition), E.N. Zalta (ed.). URL=<https://plato.stanford.edu/archives/fall2014/entries/duhem/>
- Bandy, A., 2009, Chess and Chocolate: Unlocking Lakatos, Budapest: Akadémiai Kiadó.
- Brown, M.B. and G. Priest, 2015, “Chunk and Permeate II: Bohr’s Hydrogen Atom”, European Journal for the Philosophy of Science, 5(3): 297–314. doi:10.1007/s13194-014-0104-7
- Chalmers, A.F., 2013, What Is This Thing Called Science, 4th edition, Brisbane: University of Queensland Press. First edition in 1976.
- Cohen, R.S., P.K. Feyerabend, and M.W. Wartofsky (eds.), 1976, Essays in Memory of Imre Lakatos, Boston Studies in the Philosophy of Science, 39, Dordrecht/Boston: Reidel
- Congden, L. 1997, “Possessed: Lakatos”s Road to 1956, Contemporary European History, 6(3), 279—294.
- –––, 2002, “Lakatos’s Political Reawakening” in G. Kampis et al. 2002: 339–349.
- Dostoevsky, F.M., 1994 [1871–72], Demons, R. Pevear and L. Volkhonsky (trans.), New York: Knopf.
- Feyerabend, P.K., 1968, “Consolation for the Specialist” in Lakatos (and Musgrave) 1970b: 197–230.
- –––, 1975a, “Imre Lakatos”, British Journal for the Philosophy of Science, 26: 1–18.
- –––, 1975b, Against Method, London: New Left Books.
- Flynn, J.R., 1987, “Massive IQ Gains in Fourteen Nations: What IQ Tests Really Measure” Psychological Bulletin, 101: 171–191.
- –––, 2009, What Is Intelligence: Beyond the Flynn Effect, expanded edition, Cambridge: Cambridge University Press.
- Fox, J., 1981, “Critical notice: Appraising Lakatos”, Australasian Journal of Philosophy, 59(1): 92–103. doi:10.1080/00048408112340071
- Gavroglu, K., Y. Goudaroulis, and P. Nicolaccopoulos (eds.), 1989, Imre Lakatos and Theories of Scientific Change, Boston Studies in the Philosophy of Science, 111, Dordrecht/Boston/London: Kluwer Academic Publishers.
- Godfrey-Smith, P., 2003, Theory and Reality: An Introduction to the Philosophy of Science, Chicago: University of Chicago Press.
- Hacking, I., 1983, Representing and Intervening, Cambridge: Cambridge University Press.
- Hanson, N.R., 1963, “Commentary”, in A.C. Crombie (ed), Scientific Change, London: Heinemann, 458–466.
- Hegel, W.G.F., 2008 [1820/21], The Philosophy of Right, Knox and Houlgate (trans.), Oxford: Oxford University Press.
- Howson, C. (ed.), 1976, Method and Appraisal in the Physical Sciences, Cambridge: Cambridge University Press.
- Kolakowski, L., 1978, Main Currents of Marxism (Volume 2: The Golden Age), P. Falla (trans.), Oxford: Oxford University Press.
- Kadvany, J., 2001, Imre Lakatos and the Guises of Reason, Durham and London: Duke University Press.
- Kampis, George, Ladislav Kvasz, and Michael Stöltzner (eds.), 2002, Appraising Lakatos, Dordrecht: Kluwer.
- Kuhn, T.S., 1962, The Structure of Scientific Revolutions, Chicago: University of Chicago Press.
- –––, 1970, “Reflections on My Critics”, in Lakatos (and Musgrave) 1970b: 231–278.
- –––, 1977, The Essential Tension, Chicago: University of Chicago Press.
- Larvor, B., 1998, Lakatos: An Introduction, London: Routledge
- –––, 1999, “Lakatos’ Mathematical Hegelianism” The Owl of Minerva, 31(1): 23–44. [Larvor 1999 available online]
- –––, 2001, “What is Dialectical Philosophy of Mathematics?” Philosophia Mathematica, 9(1): 212–229.
- Latsis, S.J. (ed.), 1976, Method and Appraisal in Economics, Cambridge: Cambridge University Press.
- Long, J., 1998, “Lakatos in Hungary”, Philosophy of the Social Sciences, 28: 244–311.
- –––, 2002, “The Unforgiven: Imre Lakatos’ Life in Hungary”, in G. Kampis, et al. 2002: 263–302.
- Lukács, G., 1971 [1923], History and Class Consciousness: Studies in Marxist Dialectics, R. Livingstone (trans.), Cambridge Massachusetts: MIT Press.
- –––, 2014 [1919], Tactics and Ethics 1919–1929, M. McColgan (trans.), London: Verso.
- Marx, K., 1976, Capital (Volume 1), B. Fowkes (trans.), Harmondsworth, Penguin.
- Motterlini, M. (ed.), 1999 [F&AM], For and Against Method, including Lakatos’s Lectures on Scientific Method and the Lakatos-Feyerabend Correspondence, Chicago: University of Chicago Press.
- Musgrave, A.E., 1976, “Method or Madness” in R.S. Cohen, et al. 1976: 457–491.
- –––, 1983, “Facts and Values in Science Studies”, in R.W. Home (ed), Science Under Scrutiny, Australasian Studies in History and Philosophy of Science, volume 3, Dordrecht: Reidel, pp. 49–79.
- Orwell, G., 2008 [1949], Nineteen Eighty-Four, Harmondsworth: Penguin, originally published in 1949 London: Secker & Warburg.
- Piketty, T., 2014, Capital in the Twenty-First Century, Cambridge, MA: Harvard University Press.
- Pólya, G., 1945, How to Solve It, Princeton: Princeton University Press.
- Popper, K.R., 1963 [C&R], Conjectures and Refutations: The Growth of Scientific Knowledge, London: Routledge.
- –––, 1966, The Open Society and Its Enemies, 5th edition (2 Volumes), London: Routledge. First edition in 1945.
- –––, 2002 [LSD], The Logic of Scientific Discovery, London: Routledge Classics; originally published as Logik der Forschung, Vienna: J. Springer, 1935.
- Priest, G., 2002, Beyond the Limits of Thought, 2nd edition, Oxford: Oxford University Press. First edition in 1995.
- –––, 2006, In Contradiction, 2nd edition, Oxford: Oxford University Press. First edition in 1987, Leiden: Martinus Nijhoff.
- Radnitzky, G. and G. Andersson (eds.), 1978, Progress and Rationality in Science (Boston Studies in the Philosophy of Science Volume 58), Dordrecht/Boston/London: Reidel
- Roplyi, L., 2002, “Lakatos and Lukács” in Kampis et al. 2002: 303–338.
- Russell, B., 2010 [1918], The Philosophy of Logical Atomism, London: Routledge.
- –––, 1944, “Reply to Criticisms”, in P. Schilpp (ed.), The Philosophy of Bertrand Russell, Evanston and Chicago: Northwestern University Press, pp. 679–741.
- Schilpp, P.A. (ed.), 1944, The Philosophy of Bertrand Russell, Evanston: North Western University Press.
- Schilpp, P.A. (ed.), 1974, The Philosophy of Karl Popper, La Salle: Open Court.
- Urbach, P., 1974, “Progress and Degeneration in the ‘IQ Debate’”, British Journal for the Philosophy of Science, 25: 99–135, 235–259.
- Zahar, E., 1973, “Why did Einstein’s Programme supersede Lorentz’s?”, British Journal for the Philosophy of Science, 24: 95–123, 223–262.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
- Lakatos, webpages on Lakatos at the London School of Economics.
- From Budapest: the story of Imre Lakatos, at the Philosopher’s Zone.


