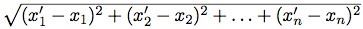Continuity and Infinitesimals
The usual meaning of the word continuous is “unbroken” or “uninterrupted”: thus a continuous entity—a continuum—has no “gaps.” We commonly suppose that space and time are continuous, and certain philosophers have maintained that all natural processes occur continuously: witness, for example, Leibniz's famous apothegm natura non facit saltus—“nature makes no jump.” In mathematics the word is used in the same general sense, but has had to be furnished with increasingly precise definitions. So, for instance, in the later 18th century continuity of a function was taken to mean that infinitesimal changes in the value of the argument induced infinitesimal changes in the value of the function. With the abandonment of infinitesimals in the 19th century this definition came to be replaced by one employing the more precise concept of limit.
Traditionally, an infinitesimal quantity is one which, while not necessarily coinciding with zero, is in some sense smaller than any finite quantity. For engineers, an infinitesimal is a quantity so small that its square and all higher powers can be neglected. In the theory of limits the term “infinitesimal” is sometimes applied to any sequence whose limit is zero. An infinitesimal magnitude may be regarded as what remains after a continuum has been subjected to an exhaustive analysis, in other words, as a continuum “viewed in the small.” It is in this sense that continuous curves have sometimes been held to be “composed” of infinitesimal straight lines.
Infinitesimals have a long and colourful history. They make an early appearance in the mathematics of the Greek atomist philosopher Democritus (c. 450 B.C.E.), only to be banished by the mathematician Eudoxus (c. 350 B.C.E.) in what was to become official “Euclidean” mathematics. Taking the somewhat obscure form of “indivisibles,” they reappear in the mathematics of the late middle ages and later played an important role in the development of the calculus. Their doubtful logical status led in the nineteenth century to their abandonment and replacement by the limit concept. In recent years, however, the concept of infinitesimal has been refounded on a rigorous basis.
- 1. Introduction: The Continuous, the Discrete, and the Infinitesimal
- 2. The Continuum and the Infinitesimal in the Ancient Period
- 3. The Continuum and the Infinitesimal in the Medieval, Renaissance, and Early Modern Periods
- 4. The Continuum and the Infinitesimal in the 17th and 18th Centuries
- 5. The Continuum and the Infinitesimal in the 19th Century
- 6. Critical Reactions to Arithmetization
- 7. Nonstandard Analysis
- 8. The Constructive Real Line and the Intuitionistic Continuum
- 9. Smooth Infinitesimal Analysis
- Bibliography
- Other Internet Resources
- Related Entries
1. Introduction: The Continuous, the Discrete, and the Infinitesimal
We are all familiar with the idea of continuity. To be continuous[1] is to constitute an unbroken or uninterrupted whole, like the ocean or the sky. A continuous entity—a continuum—has no “gaps”. Opposed to continuity is discreteness: to be discrete[2] is to be separated, like the scattered pebbles on a beach or the leaves on a tree. Continuity connotes unity; discreteness, plurality.
While it is the fundamental nature of a continuum to be undivided, it is nevertheless generally (although not invariably) held that any continuum admits of repeated or successive division without limit. This means that the process of dividing it into ever smaller parts will never terminate in an indivisible or an atom—that is, a part which, lacking proper parts itself, cannot be further divided. In a word, continua are divisible without limit or infinitely divisible. The unity of a continuum thus conceals a potentially infinite plurality. In antiquity this claim met with the objection that, were one to carry out completely—if only in imagination—the process of dividing an extended magnitude, such as a continuous line, then the magnitude would be reduced to a multitude of atoms—in this case, extensionless points—or even, possibly, to nothing at all. But then, it was held, no matter how many such points there may be—even if infinitely many—they cannot be “reassembled” to form the original magnitude, for surely a sum of extensionless elements still lacks extension[3]. Moreover, if indeed (as seems unavoidable) infinitely many points remain after the division, then, following Zeno, the magnitude may be taken to be a (finite) motion, leading to the seemingly absurd conclusion that infinitely many points can be “touched” in a finite time.
Such difficulties attended the birth, in the 5th century B.C.E., of the school of atomism. The founders of this school, Leucippus and Democritus, claimed that matter, and, more generally, extension, is not infinitely divisible. Not only would the successive division of matter ultimately terminate in atoms, that is, in discrete particles incapable of being further divided, but matter had in actuality to be conceived as being compounded from such atoms. In attacking infinite divisibility the atomists were at the same time mounting a claim that the continuous is ultimately reducible to the discrete, whether it be at the physical, theoretical, or perceptual level.
The eventual triumph of the atomic theory in physics and chemistry in the 19th century paved the way for the idea of “atomism”, as applying to matter, at least, to become widely familiar: it might well be said, to adapt Sir William Harcourt's famous observation in respect of the socialists of his day, “We are all atomists now.” Nevertheless, only a minority of philosophers of the past espoused atomism at a metaphysical level, a fact which may explain why the analogous doctrine upholding continuity lacks a familiar name: that which is unconsciously acknowledged requires no name. Peirce coined the term synechism (from Greek syneche, “continuous”) for his own philosophy—a philosophy permeated by the idea of continuity in its sense of “being connected”[4]. In this article I shall appropriate Peirce's term and use it in a sense shorn of its Peircean overtones, simply as a contrary to atomism. I shall also use the term “divisionism” for the more specific doctrine that continua are infinitely divisible.
Closely associated with the concept of a continuum is that of infinitesimal.[5] An infinitesimal magnitude has been somewhat hazily conceived as a continuum “viewed in the small,” an “ultimate part” of a continuum. In something like the same sense as a discrete entity is made up of its individual units, its “indivisibles”, so, it was maintained, a continuum is “composed” of infinitesimal magnitudes, its ultimate parts. (It is in this sense, for example, that mathematicians of the 17th century held that continuous curves are “composed” of infinitesimal straight lines.) Now the “coherence” of a continuum entails that each of its (connected) parts is also a continuum, and, accordingly, divisible. Since points are indivisible, it follows that no point can be part of a continuum. Infinitesimal magnitudes, as parts of continua, cannot, of necessity, be points: they are, in a word, nonpunctiform.
Magnitudes are normally taken as being extensive quantities, like mass or volume, which are defined over extended regions of space. By contrast, infinitesimal magnitudes have been construed as intensive magnitudes resembling locally defined intensive quantities such as temperature or density. The effect of “distributing” or “integrating” an intensive quantity over such an intensive magnitude is to convert the former into an infinitesimal extensive quantity: thus temperature is transformed into infinitesimal heat and density into infinitesimal mass. When the continuum is the trace of a motion, the associated infinitesimal/intensive magnitudes have been identified as potential magnitudes—entities which, while not possessing true magnitude themselves, possess a tendency to generate magnitude through motion, so manifesting “becoming” as opposed to “being”.
An infinitesimal number is one which, while not coinciding with zero, is in some sense smaller than any finite number. This sense has often been taken to be the failure to satisfy the Principle of Archimedes, which amounts to saying that an infinitesimal number is one that, no matter how many times it is added to itself, the result remains less than any finite number. In the engineer's practical treatment of the differential calculus, an infinitesimal is a number so small that its square and all higher powers can be neglected. In the theory of limits the term “infinitesimal” is sometimes applied to any sequence whose limit is zero.
The concept of an indivisible is closely allied to, but to be distinguished from, that of an infinitesimal. An indivisible is, by definition, something that cannot be divided, which is usually understood to mean that it has no proper parts. Now a partless, or indivisible entity does not necessarily have to be infinitesimal: souls, individual consciousnesses, and Leibnizian monads all supposedly lack parts but are surely not infinitesimal. But these have in common the feature of being unextended; extended entities such as lines, surfaces, and volumes prove a much richer source of “indivisibles”. Indeed, if the process of dividing such entities were to terminate, as the atomists maintained, it would necessarily issue in indivisibles of a qualitatively different nature. In the case of a straight line, such indivisibles would, plausibly, be points; in the case of a circle, straight lines; and in the case of a cylinder divided by sections parallel to its base, circles. In each case the indivisible in question is infinitesimal in the sense of possessing one fewer dimension than the figure from which it is generated. In the 16th and 17th centuries indivisibles in this sense were used in the calculation of areas and volumes of curvilinear figures, a surface or volume being thought of as a collection, or sum, of linear, or planar indivisibles respectively.
The concept of infinitesimal was beset by controversy from its beginnings. The idea makes an early appearance in the mathematics of the Greek atomist philosopher Democritus c. 450 B.C.E., only to be banished c. 350 B.C.E. by Eudoxus in what was to become official “Euclidean” mathematics. We have noted their reappearance as indivisibles in the sixteenth and seventeenth centuries: in this form they were systematically employed by Kepler, Galileo's student Cavalieri, the Bernoulli clan, and a number of other mathematicians. In the guise of the beguilingly named “linelets” and “timelets”, infinitesimals played an essential role in Barrow's “method for finding tangents by calculation”, which appears in his Lectiones Geometricae of 1670. As “evanescent quantities” infinitesimals were instrumental (although later abandoned) in Newton's development of the calculus, and, as “inassignable quantities”, in Leibniz's. The Marquis de l'Hôpital, who in 1696 published the first treatise on the differential calculus (entitled Analyse des Infiniments Petits pour l'Intelligence des Lignes Courbes), invokes the concept in postulating that “a curved line may be regarded as being made up of infinitely small straight line segments,” and that “one can take as equal two quantities differing by an infinitely small quantity.”
However useful it may have been in practice, the concept of infinitesimal could scarcely withstand logical scrutiny. Derided by Berkeley in the 18th century as “ghosts of departed quantities”, in the 19th century execrated by Cantor as “cholera-bacilli” infecting mathematics, and in the 20th roundly condemned by Bertrand Russell as “unnecessary, erroneous, and self-contradictory”, these useful, but logically dubious entities were believed to have been finally supplanted in the foundations of analysis by the limit concept which took rigorous and final form in the latter half of the 19th century. By the beginning of the 20th century, the concept of infinitesimal had become, in analysis at least, a virtual “unconcept”.
Nevertheless the proscription of infinitesimals did not succeed in extirpating them; they were, rather, driven further underground. Physicists and engineers, for example, never abandoned their use as a heuristic device for the derivation of correct results in the application of the calculus to physical problems. Differential geometers of the stature of Lie and Cartan relied on their use in the formulation of concepts which would later be put on a “rigorous” footing. And, in a technical sense, they lived on in the algebraists' investigations of nonarchimedean fields.
A new phase in the long contest between the continuous and the discrete has opened in the past few decades with the refounding of the concept of infinitesimal on a solid basis. This has been achieved in two essentially different ways, the one providing a rigorous formulation of the idea of infinitesimal number, the other of infinitesimal magnitude.
First, in the nineteen sixties Abraham Robinson, using methods of mathematical logic, created nonstandard analysis, an extension of mathematical analysis embracing both “infinitely large” and infinitesimal numbers in which the usual laws of the arithmetic of real numbers continue to hold, an idea which, in essence, goes back to Leibniz. Here by an infinitely large number is meant one which exceeds every positive integer; the reciprocal of any one of these is infinitesimal in the sense that, while being nonzero, it is smaller than every positive fraction 1/n. Much of the usefulness of nonstandard analysis stems from the fact that within it every statement of ordinary analysis involving limits has a succinct and highly intuitive translation into the language of infinitesimals.
The second development in the refounding of the concept of infinitesimal took place in the nineteen seventies with the emergence of synthetic differential geometry, also known as smooth infinitesimal analysis. Based on the ideas of the American mathematician F. W. Lawvere, and employing the methods of category theory, smooth infinitesimal analysis provides an image of the world in which the continuous is an autonomous notion, not explicable in terms of the discrete. It provides a rigorous framework for mathematical analysis in which every function between spaces is smooth (i.e., differentiable arbitrarily many times, and so in particular continuous) and in which the use of limits in defining the basic notions of the calculus is replaced by nilpotent infinitesimals, that is, of quantities so small (but not actually zero) that some power—most usefully, the square—vanishes. Smooth infinitesimal analysis embodies a concept of intensive magnitude in the form of infinitesimal tangent vectors to curves. A tangent vector to a curve at a point p on it is a short straight line segment l passing through the point and pointing along the curve. In fact we may take l actually to be an infinitesimal part of the curve. Curves in smooth infinitesimal analysis are “locally straight” and accordingly may be conceived as being “composed of” infinitesimal straight lines in de l'Hôpital's sense, or as being “generated” by an infinitesimal tangent vector.
The development of nonstandard and smooth infinitesimal analysis has breathed new life into the concept of infinitesimal, and—especially in connection with smooth infinitesimal analysis—supplied novel insights into the nature of the continuum.
2. The Continuum and the Infinitesimal in the Ancient Period
The opposition between Continuity and Discreteness played a significant role in ancient Greek philosophy. This probably derived from the still more fundamental question concerning the One and the Many, an antithesis lying at the heart of early Greek thought (see Stokes [1971]). The Greek debate over the continuous and the discrete seems to have been ignited by the efforts of Eleatic philosophers such as Parmenides (c. 515 B.C.E.), and Zeno (c. 460 B.C.E.) to establish their doctrine of absolute monism[6]. They were concerned to show that the divisibility of Being into parts leads to contradiction, so forcing the conclusion that the apparently diverse world is a static, changeless unity.[7] In his Way of Truth Parmenides asserts that Being is homogeneous and continuous. However in asserting the continuity of Being Parmenides is likely no more than underscoring its essential unity. Parmenides seems to be claiming that Being is more than merely continuous—that it is, in fact, a single whole, indeed an indivisible whole. The single Parmenidean existent is a continuum without parts, at once a continuum and an atom. If Parmenides was a synechist, his absolute monism precluded his being at the same time a divisionist.
In support of Parmenides' doctrine of changelessness Zeno formulated his famous paradoxes of motion. (see entry on Zeno's paradoxes) The Dichotomy and Achilles paradoxes both rest explicitly on the limitless divisibility of space and time.
The doctrine of Atomism,[8] which seems to have arisen as an attempt at escaping the Eleatic dilemma, was first and foremost a physical theory. It was mounted by Leucippus (fl. 440 B.C.E.) and Democritus (b. 460–457 B.C.E.) who maintained that matter was not divisible without limit, but composed of indivisible, solid, homogeneous, spatially extended corpuscles, all below the level of visibility.
Atomism was challenged by Aristotle (384–322 B.C.E.), who was the first to undertake the systematic analysis of continuity and discreteness. A thoroughgoing synechist, he maintained that physical reality is a continuous plenum, and that the structure of a continuum, common to space, time and motion, is not reducible to anything else. His answer to the Eleatic problem was that continuous magnitudes are potentially divisible to infinity, in the sense that they may be divided anywhere, though they cannot be divided everywhere at the same time.
Aristotle identifies continuity and discreteness as attributes applying to the category of Quantity[9]. As examples of continuous quantities, or continua, he offers lines, planes, solids (i.e., solid bodies), extensions, movement, time and space; among discrete quantities he includes number[10] and speech[11]. He also lays down definitions of a number of terms, including continuity. In effect, Aristotle defines continuity as a relation between entities rather than as an attribute appertaining to a single entity; that is to say, he does not provide an explicit definition of the concept of continuum. He observes that a single continuous whole can be brought into existence by “gluing together” two things which have been brought into contact, which suggests that the continuity of a whole should derive from the way its parts “join up”. Accordingly for Aristotle quantities such as lines and planes, space and time are continuous by virtue of the fact that their constituent parts “join together at some common boundary”. By contrast no constituent parts of a discrete quantity can possess a common boundary.
One of the central theses Aristotle is at pains to defend is the irreducibility of the continuum to discreteness—that a continuum cannot be “composed” of indivisibles or atoms, parts which cannot themselves be further divided.
Aristotle sometimes recognizes infinite divisibility—the property of being divisible into parts which can themselves be further divided, the process never terminating in an indivisible—as a consequence of continuity as he characterizes the notion. But on occasion he takes the property of infinite divisibility as defining continuity. It is this definition of continuity that figures in Aristotle's demonstration of what has come to be known as the isomorphism thesis, which asserts that either magnitude, time and motion are all continuous, or they are all discrete.
The question of whether magnitude is perpetually divisible into smaller units, or divisible only down to some atomic magnitude leads to the dilemma of divisibility (see Miller [1982]), a difficulty that Aristotle necessarily had to face in connection with his analysis of the continuum. In the dilemma's first, or nihilistic horn, it is argued that, were magnitude everywhere divisible, the process of carrying out this division completely would reduce a magnitude to extensionless points, or perhaps even to nothingness. The second, or atomistic, horn starts from the assumption that magnitude is not everywhere divisible and leads to the equally unpalatable conclusion (for Aristotle, at least) that indivisible magnitudes must exist.
As a thoroughgoing materialist, Epicurus[12] (341–271 B.C.E.) could not accept the notion of potentiality on which Aristotle's theory of continuity rested, and so was propelled towards atomism in both its conceptual and physical senses. Like Leucippus and Democritus, Epicurus felt it necessary to postulate the existence of physical atoms, but to avoid Aristotle's strictures he proposed that these should not be themselves conceptually indivisible, but should contain conceptually indivisible parts. Aristotle had shown that a continuous magnitude could not be composed of points, that is, indivisible units lacking extension, but he had not shown that an indivisible unit must necessarily lack extension. Epicurus met Aristotle's argument that a continuum could not be composed of such indivisibles by taking indivisibles to be partless units of magnitude possessing extension.
In opposition to the atomists, the Stoic philosophers Zeno of Cition (fl. 250 B.C.E.) and Chrysippus (280–206 B.C.E.) upheld the Aristotelian position that space, time, matter and motion are all continuous (see Sambursky [1963], [1971]; White [1992]). And, like Aristotle, they explicitly rejected any possible existence of void within the cosmos. The cosmos is pervaded by a continuous invisible substance which they called pneuma (Greek: “breath”). This pneuma—which was regarded as a kind of synthesis of air and fire, two of the four basic elements, the others being earth and water—was conceived as being an elastic medium through which impulses are transmitted by wave motion. All physical occurrences were viewed as being linked through tensile forces in the pneuma, and matter itself was held to derive its qualities form the “binding” properties of the pneuma it contains.
3. The Continuum and the Infinitesimal in the Medieval, Renaissance, and Early Modern Periods
The scholastic philosophers of Medieval Europe, in thrall to the massive authority of Aristotle, mostly subscribed in one form or another to the thesis, argued with great effectiveness by the Master in Book VI of the Physics, that continua cannot be composed of indivisibles. On the other hand, the avowed infinitude of the Deity of scholastic theology, which ran counter to Aristotle's thesis that the infinite existed only in a potential sense, emboldened certain of the Schoolmen to speculate that the actual infinite might be found even outside the Godhead, for instance in the assemblage of points on a continuous line. A few scholars of the time, for example Henry of Harclay (c. 1275–1317) and Nicholas of Autrecourt (c. 1300–69) chose to follow Epicurus in upholding atomism reasonable and attempted to circumvent Aristotle's counterarguments (see Pyle [1997]).
This incipient atomism met with a determined synechist rebuttal, initiated by John Duns Scotus (c. 1266–1308). In his analysis of the problem of “whether an angel can move from place to place with a continuous motion” he offers a pair of purely geometrical arguments against the composition of a continuum out of indivisibles. One of these arguments is that if the diagonal and the side of a square were both composed of points, then not only would the two be commensurable in violation of Book X of Euclid, they would even be equal. In the other, two unequal circles are constructed about a common centre, and from the supposition that the larger circle is composed of points, part of an angle is shown to be equal to the whole, in violation of Euclid's axiom V.
William of Ockham (c. 1280–1349) brought a considerable degree of dialectical subtlety[13] to his analysis of continuity; it has been the subject of much scholarly dispute[14]. For Ockham the principal difficulty presented by the continuous is the infinite divisibility of space, and in general, that of any continuum. The treatment of continuity in the first book of his Quodlibet of 1322–7 rests on the idea that between any two points on a line there is a third—perhaps the first explicit formulation of the property of density—and on the distinction between a continuum “whose parts form a unity” from a contiguum of juxtaposed things. Ockham recognizes that it follows from the property of density that on arbitrarily small stretches of a line infinitely many points must lie, but resists the conclusion that lines, or indeed any continuum, consists of points. Concerned, rather, to determine “the sense in which the line may be said to consist or to be made up of anything.”, Ockham claims that “no part of the line is indivisible, nor is any part of a continuum indivisible.” While Ockham does not assert that a line is actually “composed” of points, he had the insight, startling in its prescience, that a punctate and yet continuous line becomes a possibility when conceived as a dense array of points, rather than as an assemblage of points in contiguous succession.
The most ambitious and systematic attempt at refuting atomism in the 14th century was mounted by Thomas Bradwardine (c. 1290 – 1349). The purpose of his Tractatus de Continuo (c. 1330) was to “prove that the opinion which maintains continua to be composed of indivisibles is false.” This was to be achieved by setting forth a number of “first principles” concerning the continuum—akin to the axioms and postulates of Euclid's Elements—and then demonstrating that the further assumption that a continuum is composed of indivisibles leads to absurdities (see Murdoch [1957]).
The views on the continuum of Nicolaus Cusanus (1401–64), a champion of the actual infinite, are of considerable interest. In his De Mente Idiotae of 1450, he asserts that any continuum, be it geometric, perceptual, or physical, is divisible in two senses, the one ideal, the other actual. Ideal division “progresses to infinity”; actual division terminates in atoms after finitely many steps.
Cusanus's realist conception of the actual infinite is reflected in his quadrature of the circle (see Boyer [1959], p. 91). He took the circle to be an infinilateral regular polygon, that is, a regular polygon with an infinite number of (infinitesimally short) sides. By dividing it up into a correspondingly infinite number of triangles, its area, as for any regular polygon, can be computed as half the product of the apothegm (in this case identical with the radius of the circle), and the perimeter. The idea of considering a curve as an infinilateral polygon was employed by a number of later thinkers, for instance, Kepler, Galileo and Leibniz.
The early modern period saw the spread of knowledge in Europe of ancient geometry, particularly that of Archimedes, and a loosening of the Aristotelian grip on thinking. In regard to the problem of the continuum, the focus shifted away from metaphysics to technique, from the problem of “what indivisibles were, or whether they composed magnitudes” to “the new marvels one could accomplish with them” (see Murdoch [1957], p. 325) through the emerging calculus and mathematical analysis. Indeed, tracing the development of the continuum concept during this period is tantamount to charting the rise of the calculus. Traditionally, geometry is the branch of mathematics concerned with the continuous and arithmetic (or algebra) with the discrete. The infinitesimal calculus that took form in the 16th and 17th centuries, which had as its primary subject matter continuous variation, may be seen as a kind of synthesis of the continuous and the discrete, with infinitesimals bridging the gap between the two. The widespread use of indivisibles and infinitesimals in the analysis of continuous variation by the mathematicians of the time testifies to the affirmation of a kind of mathematical atomism which, while logically questionable, made possible the spectacular mathematical advances with which the calculus is associated. It was thus to be the infinitesimal, rather than the infinite, that served as the mathematical stepping stone between the continuous and the discrete.
Johann Kepler (1571–1630) made abundant use of infinitesimals in his calculations. In his Nova Stereometria of 1615, a work actually written as an aid in calculating the volumes of wine casks, he regards curves as being infinilateral polygons, and solid bodies as being made up of infinitesimal cones or infinitesimally thin discs (see Baron [1987], pp. 108–116; Boyer [1969], pp. 106–110). Such uses are in keeping with Kepler's customary use of infinitesimals of the same dimension as the figures they constitute; but he also used indivisibles on occasion. He spoke, for example, of a cone as being composed of circles, and in his Astronomia Nova of 1609, the work in which he states his famous laws of planetary motion, he takes the area of an ellipse to be the “sum of the radii” drawn from the focus.
It seems to have been Kepler who first introduced the idea, which was later to become a reigning principle in geometry, of continuous change of a mathematical object, in this case, of a geometric figure. In his Astronomiae pars Optica of 1604 Kepler notes that all the conic sections are continuously derivable from one another both through focal motion and by variation of the angle with the cone of the cutting plane.
Galileo Galilei (1564–1642) advocated a form of mathematical atomism in which the influence of both the Democritean atomists and the Aristotelian scholastics can be discerned. This emerges when one turns to the First Day of Galileo's Dialogues Concerning Two New Sciences (1638). Salviati, Galileo's spokesman, maintains, contrary to Bradwardine and the Aristotelians, that continuous magnitude is made up of indivisibles, indeed an infinite number of them. Salviati/Galileo recognizes that this infinity of indivisibles will never be produced by successive subdivision, but claims to have a method for generating it all at once, thereby removing it from the realm of the potential into actual realization: this “method for separating and resolving, at a single stroke, the whole of infinity” turns out simply to the act of bending a straight line into a circle. Here Galileo finds an ingenious “metaphysical” application of the idea of regarding the circle as an infinilateral polygon. When the straight line has been bent into a circle Galileo seems to take it that that the line has thereby been rendered into indivisible parts, that is, points. But if one considers that these parts are the sides of the infinilateral polygon, they are better characterized not as indivisible points, but rather as unbendable straight lines, each at once part of and tangent to the circle[15]. Galileo does not mention this possibility, but nevertheless it does not seem fanciful to detect the germ here of the idea of considering a curve as a an assemblage of infinitesimal “unbendable” straight lines.[16]
It was Galileo's pupil and colleague Bonaventura Cavalieri (1598–1647) who refined the use of indivisibles into a reliable mathematical tool (see Boyer [1959]); indeed the “method of indivisibles” remains associated with his name to the present day. Cavalieri nowhere explains precisely what he understands by the word “indivisible”, but it is apparent that he conceived of a surface as composed of a multitude of equispaced parallel lines and of a volume as composed of equispaced parallel planes, these being termed the indivisibles of the surface and the volume respectively. While Cavalieri recognized that these “multitudes” of indivisibles must be unboundedly large, indeed was prepared to regard them as being actually infinite, he avoided following Galileo into ensnarement in the coils of infinity by grasping that, for the “method of indivisibles” to work, the precise “number” of indivisibles involved did not matter. Indeed, the essence of Cavalieri's method was the establishing of a correspondence between the indivisibles of two “similar” configurations, and in the cases Cavalieri considers it is evident that the correspondence is suggested on solely geometric grounds, rendering it quite independent of number. The very statement of Cavalieri's principle embodies this idea: if plane figures are included between a pair of parallel lines, and if their intercepts on any line parallel to the including lines are in a fixed ratio, then the areas of the figures are in the same ratio. (An analogous principle holds for solids.) Cavalieri's method is in essence that of reduction of dimension: solids are reduced to planes with comparable areas and planes to lines with comparable lengths. While this method suffices for the computation of areas or volumes, it cannot be applied to rectify curves, since the reduction in this case would be to points, and no meaning can be attached to the “ratio” of two points. For rectification a curve has, it was later realized, to be regarded as the sum, not of indivisibles, that is, points, but rather of infinitesimal straight lines, its microsegments.
René Descartes (1596–1650) employed infinitesimalist techniques, including Cavalieri's method of indivisibles, in his mathematical work. But he avoided the use of infinitesimals in the determination of tangents to curves, instead developing purely algebraic methods for the purpose. Some of his sharpest criticism was directed at those mathematicians, such as Fermat, who used infinitesimals in the construction of tangents.
As a philosopher Descartes may be broadly characterized as a synechist. His philosophical system rests on two fundamental principles: the celebrated Cartesian dualism—the division between mind and matter—and the less familiar identification of matter and spatial extension. In the Meditations Descartes distinguishes mind and matter on the grounds that the corporeal, being spatially extended, is divisible, while the mental is partless. The identification of matter and spatial extension has the consequence that matter is continuous and divisible without limit. Since extension is the sole essential property of matter and, conversely, matter always accompanies extension, matter must be ubiquitous. Descartes' space is accordingly, as it was for the Stoics, a plenum pervaded by a continuous medium.
The concept of infinitesimal had arisen with problems of a geometric character and infinitesimals were originally conceived as belonging solely to the realm of continuous magnitude as opposed to that of discrete number. But from the algebra and analytic geometry of the 16th and 17th centuries there issued the concept of infinitesimal number. The idea first appears in the work of Pierre de Fermat (see Boyer [1959]) (1601–65) on the determination of maximum and minimum (extreme) values, published in 1638.
Fermat's treatment of maxima and minima contains the germ of the fertile technique of “infinitesimal variation”, that is, the investigation of the behaviour of a function by subjecting its variables to small changes. Fermat applied this method in determining tangents to curves and centres of gravity.
4. The Continuum and the Infinitesimal in the 17th and 18th Centuries
Isaac Barrow[17] (1630–77) was one of the first mathematicians to grasp the reciprocal relation between the problem of quadrature and that of finding tangents to curves—in modern parlance, between integration and differentiation. In his Lectiones Geometricae of 1670, Barrow observes, in essence, that if the quadrature of a curve y = f(x) is known, with the area up to x given by F(x), then the subtangent to the curve y = F(x) is measured by the ratio of its ordinate to the ordinate of the original curve.
Barrow, a thoroughgoing synechist, regarded the conflict between divisionism and atomism as a live issue, and presented a number of arguments against mathematical atomism, the strongest of which is that atomism contradicts many of the basic propositions of Euclidean geometry.
Barrow conceived of continuous magnitudes as being generated by motions, and so necessarily dependent on time, a view that seems to have had a strong influence on the thinking of his illustrious pupil Isaac Newton[18] (1642–1727). Newton's meditations during the plague year 1665–66 issued in the invention of what he called the “Calculus of Fluxions”, the principles and methods of which were presented in three tracts published many years after they were written[19] : De analysi per aequationes numero terminorum infinitas; Methodus fluxionum et serierum infinitarum; and De quadratura curvarum. Newton's approach to the calculus rests, even more firmly than did Barrow's, on the conception of continua as being generated by motion.
But Newton's exploitation of the kinematic conception went much deeper than had Barrow's. In De Analysi, for example, Newton introduces a notation for the “momentary increment” (moment)—evidently meant to represent a moment or instant of time—of the abscissa or the area of a curve, with the abscissa itself representing time. This “moment”—effectively the same as the infinitesimal quantities previously introduced by Fermat and Barrow—Newton denotes by o in the case of the abscissa, and by ov in the case of the area. From the fact that Newton uses the letter v for the ordinate, it may be inferred that Newton is thinking of the curve as being a graph of velocity against time. By considering the moving line, or ordinate, as the moment of the area Newton established the generality of and reciprocal relationship between the operations of differentiation and integration, a fact that Barrow had grasped but had not put to systematic use. Before Newton, quadrature or integration had rested ultimately “on some process through which elemental triangles or rectangles were added together”, that is, on the method of indivisibles. Newton's explicit treatment of integration as inverse differentiation was the key to the integral calculus.
In the Methodus fluxionum Newton makes explicit his conception of variable quantities as generated by motions, and introduces his characteristic notation. He calls the quantity generated by a motion a fluent, and its rate of generation a fluxion. The fluxion of a fluent x is denoted by x·, and its moment, or “infinitely small increment accruing in an infinitely short time o”, by x·o. The problem of determining a tangent to a curve is transformed into the problem of finding the relationship between the fluxions x· and z· when presented with an equation representing the relationship between the fluents x and z. (A quadrature is the inverse problem, that of determining the fluents when the fluxions are given.) Thus, for example, in the case of the fluent z = xn, Newton first forms z· + z·o = (x· + x·o)n, expands the right-hand side using the binomial theorem, subtracts z = xn, divides through by o, neglects all terms still containing o, and so obtains z· = nxn−1 x·.
Newton later became discontented with the undeniable presence of infinitesimals in his calculus, and dissatisfied with the dubious procedure of “neglecting” them. In the preface to the De quadratura curvarum he remarks that there is no necessity to introduce into the method of fluxions any argument about infinitely small quantities. In their place he proposes to employ what he calls the method of prime and ultimate ratio. This method, in many respects an anticipation of the limit concept, receives a number of allusions in Newton's celebrated Principia mathematica philosophiae naturalis of 1687.
Newton developed three approaches for his calculus, all of which he regarded as leading to equivalent results, but which varied in their degree of rigour. The first employed infinitesimal quantities which, while not finite, are at the same time not exactly zero. Finding that these eluded precise formulation, Newton focussed instead on their ratio, which is in general a finite number. If this ratio is known, the infinitesimal quantities forming it may be replaced by any suitable finite magnitudes—such as velocities or fluxions—having the same ratio. This is the method of fluxions. Recognizing that this method itself required a foundation, Newton supplied it with one in the form of the doctrine of prime and ultimate ratios, a kinematic form of the theory of limits.
The philosopher-mathematician G. W. F. Leibniz[20] (1646–1716) was greatly preoccupied with the problem of the composition of the continuum—the “labyrinth of the continuum”, as he called it. Indeed we have it on his own testimony that his philosophical system—monadism—grew from his struggle with the problem of just how, or whether, a continuum can be built from indivisible elements. Leibniz asked himself: if we grant that each real entity is either a simple unity or a multiplicity, and that a multiplicity is necessarily an aggregation of unities, then under what head should a geometric continuum such as a line be classified? Now a line is extended and Leibniz held that extension is a form of repetition, so, a line, being divisible into parts, cannot be a (true) unity. It is then a multiplicity, and accordingly an aggregation of unities. But of what sort of unities? Seemingly, the only candidates for geometric unities are points, but points are no more than extremities of the extended, and in any case, as Leibniz knew, solid arguments going back to Aristotle establish that no continuum can be constituted from points. It follows that a continuum is neither a unity nor an aggregation of unities. Leibniz concluded that continua are not real entities at all; as “wholes preceding their parts” they have instead a purely ideal character. In this way he freed the continuum from the requirement that, as something intelligible, it must itself be simple or a compound of simples.
Leibniz held that space and time, as continua, are ideal, and anything real, in particular matter, is discrete, compounded of simple unit substances he termed monads.
Among the best known of Leibniz's doctrines is the Principle or Law of Continuity. In a somewhat nebulous form this principle had been employed on occasion by a number of Leibniz's predecessors, including Cusanus and Kepler, but it was Leibniz who gave to the principle “a clarity of formulation which had previously been lacking and perhaps for this reason regarded it as his own discovery” (Boyer 1959, p. 217). In a letter to Bayle of 1687, Leibniz gave the following formulation of the principle: “in any supposed transition, ending in any terminus, it is permissible to institute a general reasoning in which the final terminus may be included.” This would seem to indicate that Leibniz considered “transitions” of any kind as continuous. Certainly he held this to be the case in geometry and for natural processes, where it appears as the principle Natura non facit saltus. According to Leibniz, it is the Law of Continuity that allows geometry and the evolving methods of the infinitesimal calculus to be applicable in physics. The Principle of Continuity also furnished the chief grounds for Leibniz's rejection of material atomism.
The Principle of Continuity also played an important underlying role in Leibniz's mathematical work, especially in his development of the infinitesimal calculus. Leibniz's essays Nova Methodus of 1684 and De Geometri Recondita of 1686 may be said to represent the official births of the differential and integral calculi, respectively. His approach to the calculus, in which the use of infinitesimals, plays a central role, has combinatorial roots, traceable to his early work on derived sequences of numbers. Given a curve determined by correlated variables x, y, he wrote dx and dy for infinitesimal differences, or differentials, between the values x and y: and dy/dx for the ratio of the two, which he then took to represent the slope of the curve at the corresponding point. This suggestive, if highly formal procedure led Leibniz to evolve rules for calculating with differentials, which was achieved by appropriate modification of the rules of calculation for ordinary numbers.
Although the use of infinitesimals was instrumental in Leibniz's approach to the calculus, in 1684 he introduced the concept of differential without mentioning infinitely small quantities, almost certainly in order to avoid foundational difficulties. He states without proof the following rules of differentiation:
If a is constant, then
da = 0 d(ax) = a dx d(x+y−z) = dx + dy − dz d(xy) = x dy + y dx d(x/y) = [x dy − y dx]/y2 d(xp) = pxp−1dx, also for fractional p
But behind the formal beauty of these rules—an early manifestation of what was later to flower into differential algebra—the presence of infinitesimals makes itself felt, since Leibniz's definition of tangent employs both infinitely small distances and the conception of a curve as an infinilateral polygon.
Leibniz conceived of differentials dx, dy as variables ranging over differences. This enabled him to take the important step of regarding the symbol d as an operator acting on variables, so paving the way for the iterated application of d, leading to the higher differentials ddx = d2x, d3x = dd2x, and in general dn+1x = ddnx. Leibniz supposed that the first-order differentials dx, dy,…. were incomparably smaller than, or infinitesimal with respect to, the finite quantities x, y,…, and, in general, that an analogous relation obtained between the (n+1)th-order differentials dn+1x and the nth-order differentials dnx. He also assumed that the nth power (dx)n of a first-order differential was of the same order of magnitude as an nth-order differential dnx, in the sense that the quotient dnx/(dx)n is a finite quantity.
For Leibniz the incomparable smallness of infinitesimals derived from their failure to satisfy Archimedes' principle; and quantities differing only by an infinitesimal were to be considered equal. But while infinitesimals were conceived by Leibniz to be incomparably smaller than ordinary numbers, the Law of Continuity ensured that they were governed by the same laws as the latter.
Leibniz's attitude toward infinitesimals and differentials seems to have been that they furnished the elements from which to fashion a formal grammar, an algebra, of the continuous. Since he regarded continua as purely ideal entities, it was then perfectly consistent for him to maintain, as he did, that infinitesimal quantities themselves are no less ideal—simply useful fictions, introduced to shorten arguments and aid insight.
Although Leibniz himself did not credit the infinitesimal or the (mathematical) infinite with objective existence, a number of his followers did not hesitate to do so. Among the most prominent of these was Johann Bernoulli (1667–1748). A letter of his to Leibniz written in 1698 contains the forthright assertion that “inasmuch as the number of terms in nature is infinite, the infinitesimal exists ipso facto.” One of his arguments for the existence of actual infinitesimals begins with the positing of the infinite sequence 1/2, 1/3, 1/4,…. If there are ten terms, one tenth exists; if a hundred, then a hundredth exists, etc.; and so if, as postulated, the number of terms is infinite, then the infinitesimal exists.
Leibniz's calculus gained a wide audience through the publication in 1696, by Guillaume de L'Hôpital (1661–1704), of the first expository book on the subject, the Analyse des Infiniments Petits Pour L'Intelligence des Lignes Courbes. This is based on two definitions:
- Variable quantities are those that continually increase or decrease; and constant or standing quantities are those that continue the same while others vary.
- The infinitely small part whereby a variable quantity is continually increased or decreased is called the differential of that quantity.
And two postulates:
- Grant that two quantities, whose difference is an infinitely small quantity, may be taken (or used) indifferently for each other: or (what is the same thing) that a quantity, which is increased or decreased only by an infinitely small quantity, may be considered as remaining the same.
- Grant that a curve line may be considered as the assemblage of an infinite number of infinitely small right lines: or (what is the same thing) as a polygon with an infinite number of sides, each of an infinitely small length, which determine the curvature of the line by the angles they make with each other.
Following Leibniz, L'Hôpital writes dx for the differential of a variable quantity x. A typical application of these definitions and postulates is the determination of the differential of a product xy:
d(xy) = (x + dx)(y +dy) − xy = y dx + x dy + dx dy = y dx + x dy.
Here the last step is justified by Postulate I, since dx dy is infinitely small in comparison to y dx + x dy.
Leibniz's calculus of differentials, resting as it did on somewhat insecure foundations, soon attracted criticism. The attack mounted by the Dutch physician Bernard Nieuwentijdt[21] (1654–1718) in works of 1694-6 is of particular interest, since Nieuwentijdt offered his own account of infinitesimals which conflicts with that of Leibniz and has striking features of its own. Nieuwentijdt postulates a domain of quantities, or numbers, subject to a ordering relation of greater or less. This domain includes the ordinary finite quantities, but it is also presumed to contain infinitesimal and infinite quantities—a quantity being infinitesimal, or infinite, when it is smaller, or, respectively, greater, than any arbitrarily given finite quantity. The whole domain is governed by a version of the Archimedean principle to the effect that zero is the only quantity incapable of being multiplied sufficiently many times to equal any given quantity. Infinitesimal quantities may be characterized as quotients b/m of a finite quantity b by an infinite quantity m. In contrast with Leibniz's differentials, Nieuwentijdt's infinitesimals have the property that the product of any pair of them vanishes; in particular each infinitesimal is “nilsquare” in that its square and all higher powers are zero. This fact enables Nieuwentijdt to show that, for any curve given by an algebraic equation, the hypotenuse of the differential triangle generated by an infinitesimal abscissal increment e coincides with the segment of the curve between x and x + e. That is, a curve truly is an infinilateral polygon.
The major differences between Nieuwentijdt's and Leibniz's calculi of infinitesimals are summed up in the following table:
Leibniz Nieuwentijdt Infinitesimals are variables Infinitesimals are constants Higher-order infinitesimals exist Higher-order infinitesimals do not exist Products of infinitesimals are not absolute zeros Products of infinitesimals are absolute zeros Infinitesimals can be neglected when infinitely small with respect to other quantities (First-order) infinitesimals can never be neglected
In responding to Nieuwentijdt's assertion that squares and higher powers of infinitesimals vanish, Leibniz objected that it is rather strange to posit that a segment dx is different from zero and at the same time that the area of a square with side dx is equal to zero (Mancosu 1996, 161). Yet this oddity may be regarded as a consequence — apparently unremarked by Leibniz himself — of one of his own key principles, namely that curves may be considered as infinilateral polygons. Consider, for instance, the curve y = x2. Given that the curve is an infinilateral polygon, the infinitesimal straight stretch of the curve between the abscissae 0 and dx must coincide with the tangent to the curve at the origin — in this case, the axis of abscissae — between these two points. But then the point (dx, dx2) must lie on the axis of abscissae, which means that dx2 = 0.
Now Leibniz could retort that that this argument depends crucially on the assumption that the portion of the curve between abscissae 0 and dx is indeed straight. If this be denied, then of course it does not follow that dx2 = 0. But if one grants, as Leibniz does, that that there is an infinitesimal straight stretch of the curve (a side, that is, of an infinilateral polygon coinciding with the curve) between abscissae 0 and e, say, which does not reduce to a single point then e cannot be equated to 0 and yet the above argument shows that e2 = 0. It follows that, if curves are infinlateral polygons, then the “lengths” of the sides of these latter must be nilsquare infinitesimals. Accordingly, to do full justice to Leibniz's (as well as Nieuwentijdt's) conception, two sorts of infinitesimals are required: first, “differentials” obeying= as laid down by Leibniz — the same algebraic laws as finite quantities; and second the (necessarily smaller) nilsquare infinitesimals which measure the lengths of the sides of infinilateral polygons. It may be said that Leibniz recognized the need for the first, but not the seccond type of infinitesimal and Nieuwentijdt, vice-versa. It is of interest to note that Leibnizian infinitesimals (differentials) are realized in nonstandard analysis, and nilsquare infinitesimals in smooth infinitesimal analysis (for both types of analysis see below). In fact it has been shown to be possible to combine the two approaches, so creating an analytic framework realizing both Leibniz's and Nieuwentijdt's conceptions of infinitesimal.
The insistence that infinitesimals obey precisely the same algebraic rules as finite quantities forced Leibniz and the defenders of his differential calculus into treating infinitesimals, in the presence of finite quantities, as if they were zeros, so that, for example, x + dx is treated as if it were the same as x. This was justified on the grounds that differentials are to be taken as variable, not fixed quantities, decreasing continually until reaching zero. Considered only in the “moment of their evanescence”, they were accordingly neither something nor absolute zeros.
Thus differentials (or infinitesimals) dx were ascribed variously the four following properties:
- dx ≈ 0
- neither dx = 0 nor dx ≠ 0
- dx2 = 0
- dx → 0
where “≈” stands for “indistinguishable from”, and “→ 0” stands for “becomes vanishingly small”. Of these properties only the last, in which a differential is considered to be a variable quantity tending to 0, survived the 19th century refounding of the calculus in terms of the limit concept[22].
The leading practitioner of the calculus, indeed the leading mathematician of the 18th century, was Leonhard Euler[23] (1707–83). Philosophically Euler was a thoroughgoing synechist. Rejecting Leibnizian monadism, he favoured the Cartesian doctrine that the universe is filled with a continuous ethereal fluid and upheld the wave theory of light over the corpuscular theory propounded by Newton.
Euler rejected the concept of infinitesimal in its sense as a quantity less than any assignable magnitude and yet unequal to 0, arguing: that differentials must be zeros, and dy/dx the quotient 0/0. Since for any number α, α · 0 = 0, Euler maintained that the quotient 0/0 could represent any number whatsoever[24]. For Euler qua formalist the calculus was essentially a procedure for determining the value of the expression 0/0 in the manifold situations it arises as the ratio of evanescent increments.
But in the mathematical analysis of natural phenomena, Euler, along with a number of his contemporaries, did employ what amount to infinitesimals in the form of minute, but more or less concrete “elements” of continua, treating them not as atoms or monads in the strict sense—as parts of a continuum they must of necessity be divisible—but as being of sufficient minuteness to preserve their rectilinear shape under infinitesimal flow, yet allowing their volume to undergo infinitesimal change. This idea was to become fundamental in continuum mechanics.
While Euler treated infinitesimals as formal zeros, that is, as fixed quantities, his contemporary Jean le Rond d'Alembert (1717–83) took a different view of the matter. Following Newton's lead, he conceived of infinitesimals or differentials in terms of the limit concept, which he formulated by the assertion that one varying quantity is the limit of another if the second can approach the other more closely than by any given quantity. D'Alembert firmly rejected the idea of infinitesimals as fixed quantities, and saw the idea of limit as supplying the methodological root of the differential calculus. For d'Alembert the language of infinitesimals or differentials was just a convenient shorthand for avoiding the cumbrousness of expression required by the use of the limit concept.
Infinitesimals, differentials, evanescent quantities and the like coursed through the veins of the calculus throughout the 18th century. Although nebulous—even logically suspect—these concepts provided, faute de mieux, the tools for deriving the great wealth of results the calculus had made possible. And while, with the notable exception of Euler, many 18th century mathematicians were ill-at-ease with the infinitesimal, they would not risk killing the goose laying such a wealth of golden mathematical eggs. Accordingly they refrained, in the main, from destructive criticism of the ideas underlying the calculus. Philosophers, however, were not fettered by such constraints.
The philosopher George Berkeley (1685–1753), noted both for his subjective idealist doctrine of esse est percipi and his denial of general ideas, was a persistent critic of the presuppositions underlying the mathematical practice of his day (see Jesseph [1993]). His most celebrated broadsides were directed at the calculus, but in fact his conflict with the mathematicians went deeper. For his denial of the existence of abstract ideas of any kind went in direct opposition with the abstractionist account of mathematical concepts held by the majority of mathematicians and philosophers of the day. The central tenet of this doctrine, which goes back to Aristotle, is that the mind creates mathematical concepts by abstraction, that is, by the mental suppression of extraneous features of perceived objects so as to focus on properties singled out for attention. Berkeley rejected this, asserting that mathematics as a science is ultimately concerned with objects of sense, its admitted generality stemming from the capacity of percepts to serve as signs for all percepts of a similar form.
At first Berkeley poured scorn on those who adhere to the concept of infinitesimal. maintaining that the use of infinitesimals in deriving mathematical results is illusory, and is in fact eliminable. But later he came to adopt a more tolerant attitude towards infinitesimals, regarding them as useful fictions in somewhat the same way as did Leibniz.
In The Analyst of 1734 Berkeley launched his most sustained and sophisticated critique of infinitesimals and the whole metaphysics of the calculus. Addressed To an Infidel Mathematician[25], the tract was written with the avowed purpose of defending theology against the scepticism shared by many of the mathematicians and scientists of the day. Berkeley's defense of religion amounts to the claim that the reasoning of mathematicians in respect of the calculus is no less flawed than that of theologians in respect of the mysteries of the divine.
Berkeley's arguments are directed chiefly against the Newtonian fluxional calculus. Typical of his objections is that in attempting to avoid infinitesimals by the employment of such devices as evanescent quantities and prime and ultimate ratios Newton has in fact violated the law of noncontradiction by first subjecting a quantity to an increment and then setting the increment to 0, that is, denying that an increment had ever been present. As for fluxions and evanescent increments themselves, Berkeley has this to say:
And what are these fluxions? The velocities of evanescent increments? And what are these same evanescent increments? They are neither finite quantities nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?
Nor did the Leibnizian method of differentials escape Berkeley's strictures.
The opposition between continuity and discreteness plays a significant role in the philosophical thought of Immanuel Kant (1724–1804). His mature philosophy, transcendental idealism, rests on the division of reality into two realms. The first, the phenomenal realm, consists of appearances or objects of possible experience, configured by the forms of sensibility and the epistemic categories. The second, the noumenal realm, consists of “entities of the understanding to which no objects of experience can ever correspond”, that is, things-in-themselves.
Regarded as magnitudes, appearances are spatiotemporally extended and continuous, that is infinitely, or at least limitlessly, divisible. Space and time constitute the underlying order of phenomena, so are ultimately phenomenal themselves, and hence also continuous.
As objects of knowledge, appearances are continuous extensive magnitudes, but as objects of sensation or perception they are, according to Kant, intensive magnitudes. By an intensive magnitude Kant means a magnitude possessing a degree and so capable of being apprehended by the senses: for example brightness or temperature. Intensive magnitudes are entirely free of the intuitions of space or time, and “can only be presented as unities”. But, like extensive magnitudes, they are continuous. Moreover, appearances are always presented to the senses as intensive magnitudes.
In the Critique of Pure Reason (1781) Kant brings a new subtlety (and, it must be said, tortuousity) to the analysis of the opposition between continuity and discreteness. This may be seen in the second of the celebrated Antinomies in that work, which concerns the question of the mereological composition of matter, or extended substance. Is it (a) discrete, that is, consists of simple or indivisible parts, or (b) continuous, that is, contains parts within parts ad infinitum? Although (a), which Kant calls the Thesis and (b) the Antithesis would seem to contradict one another, Kant offers proofs of both assertions. The resulting contradiction may be resolved, he asserts, by observing that while the antinomy “relates to the division of appearances”, the arguments for (a) and (b) implicitly treat matter or substance as things-in-themselves. Kant concludes that both Thesis and Antithesis “presuppose an inadmissible condition” and accordingly “both fall to the ground, inasmuch as the condition, under which alone either of them can be maintained, itself falls.”
Kant identifies the inadmissible condition as the implicit taking of matter as a thing-in-itself, which in turn leads to the mistake of taking the division of matter into parts to subsist independently of the act of dividing. In that case, the Thesis implies that the sequence of divisions is finite; the Antithesis, that it is infinite. These cannot be both be true of the completed (or at least completable) sequence of divisions which would result from taking matter or substance as a thing-in-itself.[26] Now since the truth of both assertions has been shown to follow from that assumption, it must be false, that is, matter and extended substance are appearances only. And for appearances, Kant maintains, divisions into parts are not completable in experience, with the result that such divisions can be considered, in a startling phrase, “neither finite nor infinite”. It follows that, for appearances, both Thesis and Antithesis are false.
Later in the Critique Kant enlarges on the issue of divisibility, asserting that, while each part generated by a sequence of divisions of an intuited whole is given with the whole, the sequence's incompletability prevents it from forming a whole; a fortiori no such sequence can be claimed to be actually infinite.
5. The Continuum and the Infinitesimal in the 19th Century
The rapid development of mathematical analysis in the 18th century had not concealed the fact that its underlying concepts not only lacked rigorous definition, but were even (e.g., in the case of differentials and infinitesimals) of doubtful logical character. The lack of precision in the notion of continuous function—still vaguely understood as one which could be represented by a formula and whose associated curve could be smoothly drawn—had led to doubts concerning the validity of a number of procedures in which that concept figured. For example it was often assumed that every continuous function could be expressed as an infinite series by means of Taylor's theorem. Early in the 19th century this and other assumptions began to be questioned, thereby initiating an inquiry into what was meant by a function in general and by a continuous function in particular.
A pioneer in the matter of clarifying the concept of continuous function was the Bohemian priest, philosopher and mathematician Bernard Bolzano (1781–1848). In his Rein analytischer Beweis of 1817 he defines a (real-valued) function f to be continuous at a point x if the difference f(x + ω) − f(x) can be made smaller than any preselected quantity once we are permitted to take w as small as we please. This is essentially the same as the definition of continuity in terms of the limit concept given a little later by Cauchy. Bolzano also formulated a definition of the derivative of a function free of the notion of infinitesimal (see Bolzano [1950]). Bolzano repudiated Euler's treatment of differentials as formal zeros in expressions such as dy/dx, suggesting instead that in determining the derivative of a function, increments Δx, Δy, …, be finally set to zero. For Bolzano differentials have the status of “ideal elements”, purely formal entities such as points and lines at infinity in projective geometry, or (as Bolzano himself mentions) imaginary numbers, whose use will never lead to false assertions concerning “real” quantities.
Although Bolzano anticipated the form that the rigorous formulation of the concepts of the calculus would assume, his work was largely ignored in his lifetime. The cornerstone for the rigorous development of the calculus was supplied by the ideas—essentially similar to Bolzano's—of the great French mathematician Augustin-Louis Cauchy (1789–1857). In Cauchy's work, as in Bolzano's, a central role is played by a purely arithmetical concept of limit freed of all geometric and temporal intuition. Cauchy also formulates the condition for a sequence of real numbers to converge to a limit, and states his familiar criterion for convergence[27] , namely, that a sequence <sn> is convergent if and only if sn+r − sn can be made less in absolute value than any preassigned quantity for all r and sufficiently large n. Cauchy proves that this is necessary for convergence, but as to sufficiency of the condition merely remarks “when the various conditions are fulfilled, the convergence of the series is assured.” In making this latter assertion he is implicitly appealing to geometric intuition, since he makes no attempt to define real numbers, observing only that irrational numbers are to be regarded as the limits of sequences of rational numbers.
Cauchy chose to characterize the continuity of functions in terms of a rigorized notion of infinitesimal, which he defines in the Cours d'analyse as “a variable quantity [whose value] decreases indefinitely in such a way as to converge to the limit 0.” Here is his definition of continuity. Cauchy's definition of continuity of f(x) in the neighbourhood of a value a amounts to the condition, in modern notation, that limx→af(x) = f(a). Cauchy defines the derivative f ′(x) of a function f(x) in a manner essentially identical to that of Bolzano.
The work of Cauchy (as well as that of Bolzano) represents a crucial stage in the renunciation by mathematicians—adumbrated in the work of d'Alembert—of (fixed) infinitesimals and the intuitive ideas of continuity and motion. Certain mathematicians of the day, such as Poisson and Cournot, who regarded the limit concept as no more than a circuitous substitute for the use of infinitesimally small magnitudes—which in any case (they claimed) had a real existence—felt that Cauchy's reforms had been carried too far. But traces of the traditional ideas did in fact remain in Cauchy's formulations, as evidenced by his use of such expressions as “variable quantities”, “infinitesimal quantities”, “approach indefinitely”, “as little as one wishes” and the like[28].
Meanwhile the German mathematician Karl Weierstrass (1815–97) was completing the banishment of spatiotemporal intuition, and the infinitesimal, from the foundations of analysis. To instill complete logical rigour Weierstrass proposed to establish mathematical analysis on the basis of number alone, to “arithmetize”[29] it—in effect, to replace the continuous by the discrete. “Arithmetization” may be seen as a form of mathematical atomism. In pursuit of this goal Weierstrass had first to formulate a rigorous “arithmetical” definition of real number. He did this by defining a (positive) real number to be a countable set of positive rational numbers for which the sum of any finite subset always remains below some preassigned bound, and then specifying the conditions under which two such “real numbers” are to be considered equal, or strictly less than one another.
Weierstrass was concerned to purge the foundations of analysis of all traces of the intuition of continuous motion—in a word, to replace the variable by the static. For Weierstrass a variable x was simply a symbol designating an arbitrary member of a given set of numbers, and a continuous variable one whose corresponding set S has the property that any interval around any member x of S contains members of S other than x. Weierstrass also formulated the familiar (ε, δ) definition of continuous function[30] : a function f(x) is continuous at a if for any ε > 0 there is a δ > 0 such that |f(x) − f(a)| < ε for all x such that |x − a| < δ.[31]
Following Weierstrass's efforts, another attack on the problem of formulating rigorous definitions of continuity and the real numbers was mounted by Richard Dedekind (1831–1916). Dedekind focussed attention on the question: exactly what is it that distinguishes a continuous domain from a discontinuous one? He seems to have been the first to recognize that the property of density, possessed by the ordered set of rational numbers, is insufficient to guarantee continuity. In Continuity and Irrational Numbers (1872) he remarks that when the rational numbers are associated to points on a straight line, “there are infinitely many points [on the line] to which no rational number corresponds” so that the rational numbers manifest “a gappiness, incompleteness, discontinuity”, in contrast with the straight line's “absence of gaps, completeness, continuity.” Dedekind regards this principle as being essentially indemonstrable; he ascribes to it, rather, the status of an axiom “by which we attribute to the line its continuity, by which we think continuity into the line.” It is not, Dedekind stresses, necessary for space to be continuous in this sense, for “many of its properties would remain the same even if it were discontinuous.”
The filling-up of gaps in the rational numbers through the “creation of new point-individuals” is the key idea underlying Dedekind's construction of the domain of real numbers. He first defines a cut to be a partition (A1, A2) of the rational numbers such that every member of A1 is less than every member of A2. After noting that each rational number corresponds, in an evident way, to a cut, he observes that infinitely many cuts fail to be engendered by rational numbers. The discontinuity or incompleteness of the domain of rational numbers consists precisely in this latter fact.
It is to be noted that Dedekind does not identify irrational numbers
with cuts; rather, each irrational number is newly
“created” by a mental act, and remains quite distinct from
its associated cut. Dedekind goes on to show how the domain of cuts,
and thereby the associated domain of real numbers, can be ordered in
such a way as to possess the property of continuity, viz.
“if the system ℜ
of all real numbers divides into two classes
 1,
1,
 s such
that every number a1 of the class
s such
that every number a1 of the class
 1 is
less than every number a2 of the class
1 is
less than every number a2 of the class
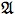 2, then
there exists one and only one number by which this separation is
produced.”
2, then
there exists one and only one number by which this separation is
produced.”
The most visionary “arithmetizer” of all was Georg Cantor[32] (1845–1918). Cantor's analysis of the continuum in terms of infinite point sets led to his theory of transfinite numbers and to the eventual freeing of the concept of set from its geometric origins as a collection of points, so paving the way for the emergence of the concept of general abstract set central to today's mathematics. Like Weierstrass and Dedekind, Cantor aimed to formulate an adequate definition of the real numbers which avoided the presupposition of their prior existence, and he follows them in basing his definition on the rational numbers. Following Cauchy, he calls a sequence a1, a2,…, an,… of rational numbers a fundamental sequence if there exists an integer N such that, for any positive rational ε, there exists an integer N such that |an+m − an| < ε for all m and all n > N. Any sequence <an> satisfying this condition is said to have a definite limit b. Dedekind had taken irrational numbers to be “mental objects” associated with cuts, so, analogously, Cantor regards these definite limits, as nothing more than formal symbols associated with fundamental sequences. The domain B of such symbols may be considered an enlargement of the domain A of rational numbers. After imposing an arithmetical structure on the domain B, Cantor is emboldened to refer to its elements as (real) numbers. Nevertheless, he still insists that these “numbers” have no existence except as representatives of fundamental sequences. Cantor then shows that each point on the line corresponds to a definite element of B. Conversely, each element of B should determine a definite point on the line. Realizing that the intuitive nature of the linear continuum precludes a rigorous proof of this property, Cantor simply assumes it as an axiom, just as Dedekind had done in regard to his principle of continuity.
For Cantor, who began as a number-theorist, and throughout his career cleaved to the discrete, it was numbers, rather than geometric points, that possessed objective significance. Indeed the isomorphism between the discrete numerical domain B and the linear continuum was regarded by Cantor essentially as a device for facilitating the manipulation of numbers.
Cantor's arithmetization of the continuum had the following important consequence. It had long been recognized that the sets of points of any pair of line segments, even if one of them is infinite in length, can be placed in one-one correspondence. This fact was taken to show that such sets of points have no well-defined “size”. But Cantor's identification of the set of points on a linear continuum with a domain of numbers enabled the sizes of point sets to be compared in a definite way, using the well-grounded idea of one-one correspondence between sets of numbers.
Cantor's investigations into the properties of subsets of the linear continuum are presented in six masterly papers published during 1879–84, Über unendliche lineare Punktmannigfaltigkeiten (“On infinite, linear point manifolds”). Remarkable in their richness of ideas, these papers provide the first accounts of Cantor's revolutionary theory of infinite sets and its application to the classification of subsets of the linear continuum. In the fifth of these papers, the Grundlagen of 1883,[33] are to be found some of Cantor's most searching observations on the nature of the continuum.
Cantor begins his examination of the continuum with a tart summary of the controversies that have traditionally surrounded the notion, remarking that the continuum has until recently been regarded as an essentially unanalyzable concept. It is Cantor's concern to “develop the concept of the continuum as soberly and briefly as possible, and only with regard to the mathematical theory of sets”. This opens the way, he believes, to the formulation of an exact concept of the continuum. Cantor points out that the idea of the continuum has heretofore merely been presupposed by mathematicians concerned with the analysis of continuous functions and the like, and has “not been subjected to any more thorough inspection.”
Repudiating any use of spatial or temporal intuition in an exact determination of the continuum, Cantor undertakes its precise arithmetical definition. Making reference to the definition of real number he has already provided (i.e., in terms of fundamental sequences), he introduces the n-dimensional arithmetical space Gn as the set of all n-tuples of real numbers <x1,x2,…,xn>, calling each such an arithmetical point of Gn. The distance between two such points is given by
Cantor defines an arithmetical point-set in Gn to be any “aggregate of points of the points of the space Gn that is given in a lawlike way”.
After remarking that he has previously shown that all spaces Gn have the same power as the set of real numbers in the interval (0,1), and reiterating his conviction that any infinite point sets has either the power of the set of natural numbers or that of (0,1),[34] Cantor turns to the definition of the general concept of a continuum within Gn.. For this he employs the concept of derivative or derived set of a point set introduced in a paper of 1872 on trigonometric series. Cantor had defined the derived set of a point set P to be the set of limit points of P, where a limit point of P is a point of P with infinitely many points of P arbitrarily close to it. A point set is called perfect if it coincides with its derived set[35]. Cantor observes that this condition does not suffice to characterize a continuum, since perfect sets can be constructed in the linear continuum which are dense in no interval, however small: as an example of such a set he offers the set[36] consisting of all real numbers in (0,1) whose ternary expansion does not contain a “1”.
Accordingly an additional condition is needed to define a continuum. Cantor supplies this by introducing the concept of a connected set. A point set T is connected in Cantor's sense if for any pair of its points t, t′ and any arbitrarily small number ε there is a finite sequence of points t1, t2,…, tn of T for which the distances [tt1], [t1t2], [t2t3], …, [t nt′], are all less than ε. Cantor now defines a continuum to be a perfect connected point set.
Cantor has advanced beyond his predecessors in formulating what is in essence a topological definition of continuum, one that, while still dependent on metric notions, does not involve an order relation[37]. It is interesting to compare Cantor's definition with the definition of continuum in modern general topology. In a well-known textbook (see Hocking and Young [1961]) on the subject we find a continuum defined as a compact connected subset of a topological space. Now within any bounded region of Euclidean space it can be shown that Cantor's continua coincide with continua in the sense of the modern definition. While Cantor lacked the definition of compactness, his requirement that continua be “complete” (which led to his rejecting as continua such noncompact sets as open intervals or discs) is not far away from the idea.
Throughout Cantor's mathematical career he maintained an unwavering, even dogmatic opposition to infinitesimals, attacking the efforts of mathematicians such as du Bois-Reymond and Veronese[38] to formulate rigorous theories of actual infinitesimals. As far as Cantor was concerned, the infinitesimal was beyond the realm of the possible; infiinitesimals were no more than “castles in the air, or rather just nonsense”, to be classed “with circular squares and square circles”. His abhorrence of infinitesimals went so deep as to move him to outright vilification, branding them as “Cholera-bacilli of mathematics.” Cantor's rejection of infinitesimals stemmed from his conviction that his own theory of transfinite ordinal and cardinal numbers exhausted the realm of the numerable, so that no further generalization of the concept of number, in particular any which embraced infinitesimals, was admissible.
6. Critical Reactions to Arithmetization
Despite the great success of Weierstrass, Dedekind and Cantor in constructing the continuum from arithmetical materials, a number of thinkers of the late 19th and early 20th centuries remained opposed, in varying degrees, to the idea of explicating the continuum concept entirely in discrete terms. These include the philosophers Brentano and Peirce and the mathematicians Poincaré, Brouwer and Weyl.
In his later years the Austrian philosopher Franz Brentano (1838–1917) became preoccupied with the nature of the continuous (see Brentano [1988]). In its fundamentals Brentano's account of the continuous is akin to Aristotle's. Brentano regards continuity as something given in perception, primordial in nature, rather than a mathematical construction. He held that the idea of the continuous is abstracted from sensible intuition. Brentano suggests that the continuous is brought to appearance by sensible intuition in three phases. First, sensation presents us with objects having parts that coincide. From such objects the concept of boundary is abstracted in turn, and then one grasps that these objects actually contain coincident boundaries. Finally one sees that this is all that is required in order to have grasped the concept of a continuum.
For Brentano the essential feature of a continuum is its inherent capacity to engender boundaries, and the fact that such boundaries can be grasped as coincident. Boundaries themselves possess a quality which Brentano calls plerosis (“fullness”). Plerosis is the measure of the number of directions in which the given boundary actually bounds. Thus, for example, within a temporal continuum the endpoint of a past episode or the starting point of a future one bounds in a single direction, while the point marking the end of one episode and the beginning of another may be said to bound doubly. In the case of a spatial continuum there are numerous additional possibilities: here a boundary may bound in all the directions of which it is capable of bounding, or it may bound in only some of these directions. In the former case, the boundary is said to exist in full plerosis; in the latter, in partial plerosis. Brentano believed that the concept of plerosis enabled sense to be made of the idea that a boundary possesses “parts”, even when the boundary lacks dimensions altogether, as in the case of a point. Thus, while the present or “now” is, according to Brentano, temporally unextended and exists only as a boundary between past and future, it still possesses two “parts” or aspects: it is both the end of the past and the beginning of the future. It is worth mentioning that for Brentano it was not just the “now” that existed only as a boundary; since, like Aristotle he held that “existence” in the strict sense means “existence now”, it necessarily followed that existing things exist only as boundaries of what has existed or of what will exist, or both.
Brentano took a somewhat dim view of the efforts of mathematicians to construct the continuum from numbers. His attitude varied from rejecting such attempts as inadequate to according them the status of “fictions”[39]. This is not surprising given his Aristotelian inclination to take mathematical and physical theories to be genuine descriptions of empirical phenomena rather than idealizations: in his view, if such theories were to be taken as literal descriptions of experience, they would amount to nothing better than “misrepresentations”.
Brentano's analysis of the continuum centred on its phenomenological and qualitative aspects, which are by their very nature incapable of reduction to the discrete. Brentano's rejection of the mathematicians' attempts to construct it in discrete terms is thus hardly surprising.
The American philosopher-mathematician Charles Sanders Peirce's (1839–1914) view of the continuum[40] was, in a sense, intermediate between that of Brentano and the arithmetizers. Like Brentano, he held that the cohesiveness of a continuum rules out the possibility of it being a mere collection of discrete individuals, or points, in the usual sense. And even before Brouwer Peirce seems to have been aware that a faithful account of the continuum will involve questioning the law of excluded middle. Peirce also held that any continuum harbours an unboundedly large collection of points—in his colourful terminology, a supermultitudinous collection—what we would today call a proper class. Peirce maintained that if “enough” points were to be crowded together by carrying insertion of new points between old to its ultimate limit they would—through a logical “transformation of quantity into quality”—lose their individual identity and become fused into a true continuum.
Peirce's conception of the number continuum is also notable for the presence in it of an abundance of infinitesimals, Peirce championed the retention of the infinitesimal concept in the foundations of the calculus, both because of what he saw as the efficiency of infinitesimal methods, and because he regarded infinitesimals as constituting the “glue” causing points on a continuous line to lose their individual identity.
The idea of continuity played a central role in the thought of the great French mathematician Henri Poincaré[41] (1854–1912). While accepting the arithmetic definition of the continuum, he questions the fact that (as with Dedekind and Cantor's formulations) the (irrational) numbers so produced are mere symbols, detached from their origins in intuition. Unlike Cantor, Poincaré accepted the infinitesimal, even if he did not regard all of the concept's manifestations as useful.
The Dutch mathematician L. E. J. Brouwer (1881–1966) is best known as the founder of the philosophy of (neo)intuitionism (see Brouwer [1975]; van Dalen [1998]). Brouwer's highly idealist views on mathematics bore some resemblance to Kant's. For Brouwer, mathematical concepts are admissible only if they are adequately grounded in intuition, mathematical theories are significant only if they concern entities which are constructed out of something given immediately in intuition, and mathematical demonstration is a form of construction in intuition. While admitting that the emergence of noneuclidean geometry had discredited Kant's view of space, Brouwer held, in opposition to the logicists (whom he called “formalists”) that arithmetic, and so all mathematics, must derive from temporal intuition.
Initially Brouwer held without qualification that the continuum is not constructible from discrete points, but was later to modify this doctrine. In his mature thought, he radically transformed the concept of point, endowing points with sufficient fluidity to enable them to serve as generators of a “true” continuum. This fluidity was achieved by admitting as “points”, not only fully defined discrete numbers such as √2, π, e, and the like—which have, so to speak, already achieved “being”—but also “numbers” which are in a perpetual state of becoming in that their the entries in their decimal (or dyadic) expansions are the result of free acts of choice by a subject operating throughout an indefinitely extended time. The resulting choice sequences cannot be conceived as finished, completed objects: at any moment only an initial segment is known. In this way Brouwer obtained the mathematical continuum in a way compatible with his belief in the primordial intuition of time—that is, as an unfinished, indeed unfinishable entity in a perpetual state of growth, a “medium of free development”. In this conception, the mathematical continuum is indeed “constructed”, not, however, by initially shattering, as did Cantor and Dedekind, an intuitive continuum into isolated points, but rather by assembling it from a complex of continually changing overlapping parts.
The mathematical continuum as conceived by Brouwer displays a number of features that seem bizarre to the classical eye. For example, in the Brouwerian continuum the usual law of comparability, namely that for any real numbers a, b either a < b or a = b or a > b, fails. Even more fundamental is the failure of the law of excluded middle in the form that for any real numbers a, b, either a = b or a ≠ b. The failure of these seemingly unquestionable principles in turn vitiates the proofs of a number of basic results of classical analysis, for example the Bolzano-Weierstrass theorem, as well as the theorems of monotone convergence, intermediate value, least upper bound, and maximum value for continuous functions[42].
While the Brouwerian continuum may possess a number of negative features from the standpoint of the classical mathematician, it has the merit of corresponding more closely to the continuum of intuition than does its classical counterpart. Far from being bizarre, the failure of the law of excluded middle for points in the intuitionistic continuum may be seen as fitting in well with the character of the intuitive continuum.
In 1924 Brouwer showed that every function defined on a closed interval of his continuum is uniformly continuous. As a consequence the intuitionistic continuum is indecomposable, that is, cannot be split into two disjoint parts in any way whatsoever. In contrast with a discrete entity, the indecomposable Brouwerian continuum cannot be composed of its parts. Brouwer's vision of the continuum has in recent years become the subject of intensive mathematical investigation.
Hermann Weyl (1885–1955), one of most versatile mathematicians of the 20th century, was preoccupied with the nature of the continuum (see Bell [2000]). In his Das Kontinuum of 1918 he attempts to provide the continuum with an exact mathematical formulation free of the set-theoretic assumptions he had come to regard as objectionable. As he saw it, there is an unbridgeable gap between intuitively given continua (e.g., those of space, time and motion) on the one hand, and the discrete exact concepts of mathematics (e.g., that of real number) on the other. For Weyl the presence of this split meant that the construction of the mathematical continuum could not simply be “read off” from intuition. Rather, he believed that the mathematical continuum must be treated and, in the end, justified in the same way as a physical theory. However much he may have wished it, in Das Kontinuum Weyl did not aim to provide a mathematical formulation of the continuum as it is presented to intuition, which, as the quotations above show, he regarded as an impossibility (at that time at least). Rather, his goal was first to achieve consistency by putting the arithmetical notion of real number on a firm logical basis, and then to show that the resulting theory is reasonable by employing it as the foundation for a plausible account of continuous process in the objective physical world.
Later Weyl came to repudiate atomistic theories of the continuum, including that of his own Das Kontinuum. He accordingly welcomed Brouwer's construction of the continuum by means of sequences generated by free acts of choice, thus identifying it as a “medium of free Becoming” which “does not dissolve into a set of real numbers as finished entities”. Weyl felt that Brouwer, through his doctrine of intuitionism, had come closer than anyone else to bridging that “unbridgeable chasm” between the intuitive and mathematical continua. In particular, he found compelling the fact that the Brouwerian continuum is not the union of two disjoint nonempty parts—that it is indecomposable. “A genuine continuum,” Weyl says, “cannot be divided into separate fragments.” In later publications he expresses this more colourfully by quoting Anaxagoras to the effect that a continuum “defies the chopping off of its parts with a hatchet.”
7. Nonstandard Analysis
Once the continuum had been provided with a set-theoretic foundation, the use of the infinitesimal in mathematical analysis was largely abandoned. And so the situation remained for a number of years. The first signs of a revival of the infinitesimal approach to analysis surfaced in 1958 with a paper by A. H. Laugwitz and C. Schmieden[43]. But the major breakthrough came in 1960 when it occurred to the mathematical logician Abraham Robinson (1918–1974) that “the concepts and methods of contemporary Mathematical Logic are capable of providing a suitable framework for the development of the Differential and Integral Calculus by means of infinitely small and infinitely large numbers.” (see Robinson [1996], p. xiii) This insight led to the creation of nonstandard analysis,[44] which Robinson regarded as realizing Leibniz's conception of infinitesimals and infinities as ideal numbers possessing the same properties as ordinary real numbers.
After Robinson's initial insight, a number of ways of presenting nonstandard analysis were developed. Here is a sketch of one of them.
Starting with the classical real line
ℜ,
a set-theoretic
universe—the standard universe—is first
constructed over it: here by such a universe is meant a set U
containing
ℜ
which
is closed under the usual set-theoretic operations of union,
power set, Cartesian products and subsets. Now write
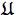 for the structure
(U, ∈), where ∈ is the usual membership relation on
U: associated with this is the extension
L(U) of
the first-order language of set theory to include a name
u for each element u of U.
Now, using the well-known compactness theorem for first-order
logic,
for the structure
(U, ∈), where ∈ is the usual membership relation on
U: associated with this is the extension
L(U) of
the first-order language of set theory to include a name
u for each element u of U.
Now, using the well-known compactness theorem for first-order
logic,
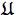 is extended
to a new structure
*
is extended
to a new structure
*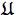 = (*U, *∈), called a nonstandard
universe, satisfying the following key principle:
= (*U, *∈), called a nonstandard
universe, satisfying the following key principle:
Saturation Principle. Let Φ be a collection of L(U)-formulas with exactly one free variable. If Φ is finitely satisfiable in, that is, if for any finite subset Φ′ of Φ there is an element of U which satisfies all the formulas of Φ′ in
, then there is an element of *U which satisfies all the formulas of Φ in *
.
The saturation property expresses the intuitive idea that the
nonstandard universe is very rich in comparison to the standard one.
Indeed, while there may exist, for each finite subcollection
F
of a given collection of properties
P,
an element of U satisfying the members
of
F in
 ,
there may not necessarily be an element of U satisfying
all the members of
P.
The saturation of
*
,
there may not necessarily be an element of U satisfying
all the members of
P.
The saturation of
* guarantees the existence of an element of
*U which satisfies, in
*
guarantees the existence of an element of
*U which satisfies, in
* ,
all the members of
P.
For example, suppose the set
ℕ
of natural numbers is a member of U; for each n
∈
ℕ
let Pn(x) be the property x
∈
ℕ
& n < x. Then clearly, while each finite
subcollection of the collection
P
= {Pn: n ∈
ℕ}
is satisfiable
in
,
all the members of
P.
For example, suppose the set
ℕ
of natural numbers is a member of U; for each n
∈
ℕ
let Pn(x) be the property x
∈
ℕ
& n < x. Then clearly, while each finite
subcollection of the collection
P
= {Pn: n ∈
ℕ}
is satisfiable
in
 , the whole
collection is not. An element of *U satisfying
P
in
*
, the whole
collection is not. An element of *U satisfying
P
in
* will then be an
“natural number” greater than every member of
ℕ,
that is, an
infinite number.
will then be an
“natural number” greater than every member of
ℕ,
that is, an
infinite number.
From the saturation property it follows that
* satisfies the
important
satisfies the
important
Transfer Principle. If σ is any sentence of L(U), then σ holds inif and only if it holds in *
.
The transfer principle may be seen as a version of Leibniz's continuity principle: it asserts that all first-order properties are preserved in the passage to or “transfer” from the standard to the nonstandard universe.
The members of U are called standard sets, or standard objects; those in *U − U nonstandard sets or nonstandard objects: *U thus consists of both standard and nonstandard objects. The members of *U will also be referred to as *-sets or *-objects Since U ⊆ *U, under this convention every set (object) is also a *-set (object) The *-members of a *-set A are the *-objects x for which x *∈ A.
If A is a standard set, we may consider the collection —the inflate of A—consisting of all the *-members of A: this is not necessarily a set nor even a *-set. The inflate  of a standard set A may be regarded as the same set A viewed from a nonstandard vantage point. While clearly A ⊆ Â,  may contain “nonstandard” elements not in A. It can in fact be shown that infinite standard sets always get “inflated” in this way. Using the transfer principle, any function f between standard sets automatically extends to a function—also written f—between their inflates.
If
 =
(A, R,…) is a mathematical structure, we may
consider the structure
=
(A, R,…) is a mathematical structure, we may
consider the structure
 =
(Â,Rˆ).
From the transfer principle it follows that
=
(Â,Rˆ).
From the transfer principle it follows that
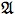 and
and
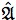 have precisely
the same first-order properties.
have precisely
the same first-order properties.
Now suppose that the set ℕ of natural numbers is a member of U. Then so is the set ℜ of real numbers, since each real number may be identified with a set of natural numbers. ℜ may be regarded as an ordered field, and the same is therefore true of its inflate ℜˆ, since the latter has precisely the same first-order properties as ℜ. ℜˆ is called the hyperreal line, and its members hyperreals. A standard hyperreal is then just a real, to which we shall refer for emphasis as a standard real. Since ℜ is infinite, nonstandard hyperreals must exist. The saturation principle implies that there must be an infinite (nonstandard) hyperreal,[45] that is, a hyperreal a such that a > n for every n ∈ ℕ. In that case its reciprocal 1/a is infinitesimal in the sense of exceeding 0 and yet being smaller than 1/n+1 for every n ∈ ℕ. In general, we call a hyperreal a infinitesimal if its absolute value |a| is less than 1/n+1 for every n ∈ ℕ. In that case the set I of infinitesimals contains not just 0 but a substantial number (in fact, infinitely many) other elements. Clearly I is an additive subgroup of ℜ, that is, if a, b ∈ I, then a − b ∈ I.
The members of the inflate ℕˆ of ℕ are called hypernatural numbers. As for the hyperreals, it can be shown that ℕˆ also contains nonstandard elements which must exceed every member of ℕ; these are called infinite hypernatural numbers.
For hyperreals a, b we define a ≈ b and say that a and b are infinitesimally close if a − b ∈ I. This is an equivalence relation on the hyperreal line: for each hyperreal a we write μ(a) for the equivalence class of a under this relation and call it the monad of a. The monad of a hyperreal a thus consists of all the hyperreals that are infinitesimally close to a: it may be thought of as a small cloud centred at a. Note also that μ(0) = I.
A hyperreal a is finite if it is not infinite; this means that |a| < n for some n ∈ ℕ . It is not difficult to show that finiteness is equivalent to the condition of near-standardness; here a hyperreal a is near-standard if a ≈ r for some standard real r.
Much of the usefulness of nonstandard analysis stems from the fact that statements of classical analysis involving limits or the (ε, δ) criterion admit succinct, intuitive translations into statements involving infinitesimals or infinite numbers, in turn enabling comparatively straightforward proofs to be given of classical theorems. Here are some examples of such translations:[46]
- Let <sn> be a standard infinite sequence of real numbers and let s be a standard real number. Then s is the limit of <sn> within ℜ, limn→∞ sn = s in the classical sense, if and only if sn ≈ s for all infinite subscripts n.
- A standard sequence <sn> converges if and only if sn ≈ sm for all infinite n and m. (Cauchy's criterion for convergence.)
Now suppose that f is a real-valued function defined on
some open interval (a, b). We have remarked above
that f automatically extends to a function—also written
f—on
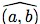
- In order that the standard real number c be the limit of f(x) as x approaches x0, limx→x0f(x) = c, with x0 a standard real number in (a, b), it is necessary and sufficient that f(x) ≈ f(x0) for all x ≈ x0.
- The function f is continuous at a standard real number x0 in (a, b) if and only if f(x) ≈ f(x0) for all x ≈ x0. (This is equivalent to saying that f maps the monad of x0 into the monad of f(x0.)
- In order that the standard number c be the derivative of
f at x0 it is necessary and sufficient
that
for all x ≠ x0 in the monad of x0.f(x) − f(x0) x − x0 ≈ c
Many other branches of mathematics admit neat and fruitful nonstandard formulations.
8. The Constructive Real Line and the Intuitionistic Continuum
The original motivation for the development of constructive mathematics was to put the idea of mathematical existence on a constructive or computable basis. While there are a number of varieties of constructive mathematics (see Bridges and Richman [1987]), here we shall focus on Bishop's constructive analysis (see Bishop and Bridges [1985]; Bridges [1994], [1999]; and Bridges and Richman [1987]) and Brouwer's intuitionistic analysis (see Dummett [1977]).
In constructive mathematics a problem is counted as solved only if an explicit solution can, in principle at least, be produced. Thus, for example, “There is an x such that P(x)” means that, in principle at least, we can explicitly produce an x such that P(x). This fact led to the questioning of certain principles of classical logic, in particular, the law of excluded middle, and the creation of a new logic, intuitionistic logic (see entry on intuitionistic logic). It also led to the introduction of a sharpened definition of real numbers—the constructive real numbers. A constructive real number is a sequence of rationals (rn) = r1, r2, … such that, for any k, a number n can be computed in such a way that |rn+p − rn| ≤ 1/k. Each rational number a may be regarded as a real number by identifying it with the real number (α, α, …). The set R of all constructive real numbers is the constructive real line.
Now of course, for any “given” real number there are a variety of ways of giving explicit approximating sequences for it. Thus it is necessary to define an equivalence relation, “equality on the reals”. The correct definition here is: r =ℜ s iff for any k, a number n can be found so that |rn+p − sn+p| ≤ 1/k, for all p. To say that two real numbers are equal is to say that they are equivalent in this sense.
The real number line can be furnished with an axiomatic description. We begin by assuming the existence of a set R with
- a binary relation > (greater than)
- a corresponding apartness relation # defined by x # y ⇔ x > y or y > x
- a unary operation x
 −x
−x - binary operations (x, y)
 x +
y (addition) and (x, y)
x +
y (addition) and (x, y)
 xy
(multiplication)
xy
(multiplication) - distinguished elements 0 (zero) and 1 (one) with 0 ≠ 1
- a unary operation x
 x−1 on the set of
elements ≠ 0.
x−1 on the set of
elements ≠ 0.
The elements of R are called real numbers. A real number x is positive if x > 0 and negative if −x > 0. The relation ≥ (greater than or equal to) is defined by
x ≥ y ⇔ ∀z(y > z ⇒ x > z).
The relations < and ≤ are defined in the usual way; x is nonnegative if 0 ≤ x. Two real numbers are equal if x ≥ y and y ≥ x, in which case we write x = y.
The sets N of natural numbers, N+ of positive integers, Z of integers and Q of rational numbers are identified with the usual subsets of R; for instance N+ is identified with the set of elements of R of the form 1 + 1 + … + 1.
These relations and operations are subject to the following three groups of axioms, which, taken together, form the system CA of axioms for constructive analysis, or the constructive real numbers (see Bridges [1999]).
Field Axioms
- x + y = y + x
- (x + y) + z = x + (y + z)
- 0 + x = x
- x + (−x) = 0 xy = yx
- (xy)z = x(yz)
- 1x = x
- xx−1 = 1 if x # 0
- x(y + z) = xy + xz
Order Axioms
- ¬(x > y ∧ y > x)
- x > y ⇒ ∀z(x > z ∨ z > y)
- ¬(x # y) ⇒ x = y
- x > y ⇒ ∀z(x + z > y + z)
- (x > 0 ∧ y > 0) ⇒ xy > 0.
The last two axioms introduce special properties of > and ≥. In the second of these the notions bounded above, bounded below, and bounded are defined as in classical mathematics, and the least upper bound, if it exists, of a nonempty[47] set S of real numbers is the unique real number b such that
- b is an upper bound for S, and
- for each c < b there exists s ∈ S with s > c.
Special Properties of >.
Archimedean axiom. For each x ∈ R such that x ≥ 0 there exists n ∈ N such that x < n.The least upper bound principle. Let S be a nonempty subset of R that is bounded above relative to the relation ≥, such that for all real numbers a, b with a < b, either b is an upper bound for S or else there exists s ∈ S with s > a. Then S has a least upper bound.
The following basic properties of > and ≥ can then be established.
- ¬(x > x)
- x ≥ x
- x > y ∧ y > z ⇒ x > z
- ¬(x > y ∧ y ≥ x)
- (x > y ≥ z) ⇒ x > z
- ¬(x > y) ⇔ y ≥ x
- ¬¬(x ≥ y) ⇔ ¬¬(y > x)
- (x ≥ y ≥ z) ⇒ x ≥ z
- (x ≥ y ∧ y ≥ x) ⇒ x = y
- ¬(x > y ∧ x = y)
- x ≥ 0 ⇔ ∀ε>0(x < ε)
- x + y > 0 ⇒ (x > 0 ∨ y > 0)
- x > 0 ⇒ −x < 0
- (x > y ∧ z < 0) ⇒ yz > xz
- x # 0 ⇒ x2 > 0
- 1 > 0
- x2 > 0
- 0 < x < 1 ⇒ x > x2
- x2 > 0 ⇒ x # 0
- n ∈ N+ ⇒ n−1 > 0
- if x > 0 and y ≥ 0, then ∃n∈Z(nx > y)
- x > 0 ⇒ x−1 > 0
- xy > 0 ⇒ (x ≠ 0 ∨ y ≠ 0)
- if a < b, then ∃r∈Q(a < r < b)
The constructive real line R as introduced above is a model of CA. Are there any other models, that is, models not isomorphic to R. If classical logic is assumed, CA is a categorical theory and so the answer is no. But this is not the case within intuitionistic logic, for there it is possible for the Dedekind and Cantor reals to fail to be isomorphic, despite the fact that they are both models of CA.
In constructive analysis, a real number is an infinite (convergent) sequence of rational numbers generated by an effective rule, so that the constructive real line is essentially just a restriction of its classical counterpart. Brouwerian intuitionism takes a more liberal view of the matter, resulting in a considerable enrichment of the arithmetical continuum over the version offered by strict constructivism. As conceived by intutionism, the arithmetical continuum admits as real numbers not only infinite sequences determined in advance by an effective rule for computing their terms, but also ones in whose generation free selection plays a part. The latter are called (free) choice sequences. Without loss of generality we may and shall assume that the entries in choice sequences are natural numbers.
While constructive analysis does not formally contradict classical analysis, and may in fact be regarded as a subtheory of the latter, a number of intuitionistically plausible principles have been proposed for the theory of choice sequences which render intuitionistic analysis divergent from its classical counterpart. One such principle is Brouwer's Continuity Principle: given a relation Q(α, n) between choice sequences α and numbers n, if for each α a number n may be determined for which Q(α, n) holds, then n can already be determined on the basis of the knowledge of a finite number of terms of α.[48] From this one can prove a weak version of the Continuity Theorem, namely, that every function from R to R is continuous. Another such principle is Bar Induction, a certain form of induction for well-founded sets of finite sequences[49]. Brouwer used Bar Induction and the Continuity Principle in proving his Continuity Theorem that every real-valued function defined on a closed interval is uniformly continuous, from which, as has already been observed, it follows that the intuitionistic continuum is indecomposable.
Brouwer gave the intuitionistic conception of mathematics an explicitly subjective twist by introducing the creative subject. The creative subject was conceived as a kind of idealized mathematician for whom time is divided into discrete sequential stages, during each of which he may test various propositions, attempt to construct proofs, and so on. In particular, it can always be determined whether or not at stage n the creative subject has a proof of a particular mathematical proposition p. While the theory of the creative subject remains controversial, its purely mathematical consequences can be obtained by a simple postulate which is entirely free of subjective and temporal elements.
The creative subject allows us to define, for a given proposition p, a binary sequence <an> by an = 1 if the creative subject has a proof of p at stage n; an = 0 otherwise. Now if the construction of these sequences is the only use made of the creative subject, then references to the latter may be avoided by postulating the principle known as Kripke's Scheme
For each proposition p there exists an increasing binary sequence <an> such that p holds if and only if an = 1 for some n.
Taken together, these principles have been shown to have remarkable consequences for the indecomposability of subsets of the continuum. Not only is the intuitionistic continuum indecomposable (that is, cannot be partitioned into two nonempty disjoint parts), but, assuming the Continuity Principle and Kripke's Scheme, it remains indecomposable even if one pricks it with a pin. The intuitionistic continuum has, as it were, a syrupy nature, so that one cannot simply take away one point. If in addition Bar Induction is assumed, then, still more surprisingly, indecomposability is maintained even when all the rational points are removed from the continuum.
Finally, it has been shown that a natural notion of infinitesimal can be developed within intuitionistic mathematics (see Vesley [1981]), the idea being that an infinitesimal should be a “very small” real number in the sense of not being known to be distinguishable—that is, strictly greater than or less than—zero.
9. Smooth Infinitesimal Analysis
A major development in the refounding of the concept of infinitesimal took place in the nineteen seventies with the emergence of synthetic differential geometry, also known as smooth infinitesimal analysis (SIA)[50]. Based on the ideas of the American mathematician F. W. Lawvere, and employing the methods of category theory, smooth infinitesimal analysis provides an image of the world in which the continuous is an autonomous notion, not explicable in terms of the discrete. It provides a rigorous framework for mathematical analysis in which every function between spaces is smooth (i.e., differentiable arbitrarily many times, and so in particular continuous) and in which the use of limits in defining the basic notions of the calculus is replaced by nilpotent infinitesimals, that is, of quantities so small (but not actually zero) that some power—most usefully, the square—vanishes. Since in SIA all functions are continuous, it embodies in a striking way Leibniz's principle of continuity Natura non facit saltus.
In what follows, we use bold R to distinguish the real line in SIA from its counterparts in classical and constructive analysis. In the usual development of the calculus, for any differentiable function f on the real line R, y = f(x), it follows from Taylor's theorem that the increment δy = f(x + δx) − f(x) in y attendant upon an increment δx in x is determined by an equation of the form
δy = f ′(x)δx + A(δx)2, (1)
where f ′(x) is the derivative of f(x) and A is a quantity whose value depends on both x and δx. Now if it were possible to take δx so small (but not demonstrably identical with 0) that (δx)2 = 0 then (1) would assume the simple form
f(x + δx) − f(x) = δy = f ′(x) δx. (2)
We shall call a quantity having the property that its square is zero a nilsquare infinitesimal or simply a microquantity. In SIA “enough” microquantities are present to ensure that equation (2) holds nontrivially for arbitrary functions f: R → R. (Of course (2) holds trivially in standard mathematical analysis because there 0 is the sole microquantity in this sense.) The meaning of the term “nontrivial” here may be explicated in following way. If we replace δx by the letter ε standing for an arbitrary microquantity, (2) assumes the form
f(x + ε) − f(x) = εf ′(x). (3)
Ideally, we want the validity of this equation to be independent of ε , that is, given x, for it to hold for all microquantities ε. In that case the derivative f ′(x) may be defined as the unique quantity D such that the equation
f(x + ε) − f(x) = εD
holds for all microquantities ε.
Setting x = 0 in this equation, we get in particular
f(ε) = f(0) + εD, (4)
for all ε. It is equation (4) that is taken as axiomatic in smooth infinitesimal analysis. Let us write Δ for the set of microquantities, that is,
Δ = {x: x ∈ R ∧ x2 = 0}.
Then it is postulated that, for any f: Δ → R, there is a unique D ∈ R such that equation (4) holds for all ε. This says that the graph of f is a straight line passing through (0, f(0)) with slope Δ. Thus any function on Δ is what mathematicians term affine, and so this postulate is naturally termed the principle of microaffineness. It means that Δ cannot be bent or broken: it is subject only to translations and rotations—and yet is not (as it would have to be in ordinary analysis) identical with a point. Δ may be thought of as an entity possessing position and attitude, but lacking true extension.
Now consider the space ΔΔ of maps from Δ to itself. It follows from the microaffineness principle that the subspace (ΔΔ)0 of ΔΔ consisting of maps vanishing at 0 is isomorphic to R[51]. The space ΔΔ is a monoid[52] under composition which may be regarded as acting on Δ by evaluation: for f ∈ ΔΔ, f · ε = f (ε). Its subspace (ΔΔ)0 is a submonoid naturally identified as the space of ratios of microquantities. The isomorphism between (ΔΔ)0 and R noted above is easily seen to be an isomorphism of monoids (where R is considered a monoid under its usual multiplication). It follows that R itself may be regarded as the space of ratios of microquantities. This was essentially the view of Euler, who regarded (real) numbers as representing the possible results of calculating the ratio 0/0. For this reason Lawvere has suggested that R be called the space of Euler reals.
If we think of a function y = f(x) as defining a curve, then, for any a, the image under f of the “microinterval” Δ + a obtained by translating Δ to a is straight and coincides with the tangent to the curve at x = a. In this sense each curve is “infinitesimally straight”.
From the principle of microaffineness we deduce the important principle of microcancellation, viz.
If εa = εb for all ε, then a = b.
For the premise asserts that the graph of the function g: Δ → R defined by g(ε) = aε has both slope a and slope b: the uniqueness condition in the principle of microaffineness then gives a = b. The principle of microcancellation supplies the exact sense in which there are “enough” infinitesimals in smooth infinitesimal analysis.
From the principle of microaffineness it also follows that all functions on R are continuous, that is, send neighbouring points to neighbouring points. Here two points x, y on R are said to be neighbours if x − y is in Δ, that is, if x and y differ by a microquantity. To see this, given f : R → R and neighbouring points x, y, note that y = x + ε with ε in Δ, so that
f(y) − f(x) = f(x + ε) − f(x) = εf ′(x).
But clearly any multiple of a microquantity is also a microquantity, so εf ′(x) is a microquantity, and the result follows.
In fact, since equation (3) holds for any f, it also holds for its derivative f ′; it follows that functions in smooth infinitesimal analysis are differentiable arbitrarily many times, thereby justifying the use of the term “smooth”.
Let us derive a basic law of the differential calculus, the product rule:
(fg)′ = f ′g + fg′.
To do this we compute
(fg)(x + ε) = (fg)(x) + ε(fg)′(x) = f(x)g(x) + ε(fg)′(x),(fg)(x + ε) = f(x + ε)g(x + ε) = [f(x) + f ′(x)]·[g(x) + g′(x)]
= f(x)g(x) + ε(f ′g + fg′) + ε2f ′g′
= f(x)g(x) + ε(f ′g + fg′),
since ε2 = 0. Therefore ε(fg)′ = ε(f ′g + fg′), and the result follows by microcancellation.
A stationary point a in R of a function f : R → R is defined to be one in whose vicinity “infinitesimal variations” fail to change the value of f, that is, such that f(a + ε) = f(a) for all ε. This means that f(a) + εf ′(a)= f(a), so that εf ′(a) = 0 for all ε, whence it follows from microcancellation that f ′(a) = 0. This is Fermat's rule.
An important postulate concerning stationary points that we adopt in smooth infinitesimal analysis is the
Constancy Principle. If every point in an interval J is a stationary point of f : J → R (that is, if f ′ is identically 0), then f is constant.
Put succinctly, “universal local constancy implies global constancy”. It follows from this that two functions with identical derivatives differ by at most a constant.
In ordinary analysis the continuum R is connected in the sense that it cannot be split into two non empty subsets neither of which contains a limit point of the other. In smooth infinitesimal analysis it has the vastly stronger property of indecomposability: it cannot be split in any way whatsoever into two disjoint nonempty subsets. For suppose R = U ∪ V with U ∩ V = ∅. Define f : R → {0, 1} by f(x) = 1 if x ∈ U, f(x) = 0 if x ∈ V. We claim that f is constant. For we have
(f(x) = 0 or f(x) = 1) & (f(x + ε) = 0 or f(x + ε) = 1).
This gives 4 possibilities:
(i) f(x) = 0 & f(x + ε) = 0(ii) f(x) = 0 & f(x + ε) = 1
(iii) f(x) = 1 & f(x + ε) = 0
(iv) f(x) = 1 & f(x + ε) = 1
Possibilities (ii) and (iii) may be ruled out because f is continuous. This leaves (i) and (iv), in either of which f(x) = f(x + ε). So f is locally, and hence globally, constant, that is, constantly 1 or 0. In the first case V = ∅ , and in the second U = ∅.
We observe that the postulates of smooth infinitesimal analysis are incompatible with the law of excluded middle of classical logic. This incompatibility can be demonstrated in two ways, one informal and the other rigorous. First the informal argument. Consider the function f defined for real numbers x by f(x) = 1 if x = 0 and f(x) = 0 whenever x ≠ 0. If the law of excluded middle held, each real number would then be either equal or unequal to 0, so that the function f would be defined on the whole of R. But, considered as a function with domain R, f is clearly discontinuous. Since, as we know, in smooth infinitesimal analysis every function on R is continuous, f cannot have domain R there[53]. So the law of excluded middle fails in smooth infinitesimal analysis. To put it succinctly, universal continuity implies the failure of the law of excluded middle.
Here now is the rigorous argument. We show that the failure of the law of excluded middle can be derived from the principle of infinitesimal cancellation. To begin with, if x ≠ 0, then x2 ≠ 0, so that, if x2 = 0, then necessarily not x ≠ 0. This means that
for all infinitesimal ε, not ε ≠ 0. (*)
Now suppose that the law of excluded middle were to hold. Then we would have, for any ε, either ε = 0 or ε ≠ 0. But (*) allows us to eliminate the second alternative, and we infer that, for all ε, ε = 0. This may be written
for all ε, ε·1 = ε·0,
from which we derive by microcancellation the falsehood 1 = 0. So again the law of excluded middle must fail.
The “internal” logic of smooth infinitesimal analysis is accordingly not full classical logic. It is, instead, intuitionistic logic, that is, the logic derived from the constructive interpretation of mathematical assertions. In our brief sketch we did not notice this “change of logic” because, like much of elementary mathematics, the topics we discussed are naturally treated by constructive means such as direct computation.
What are the algebraic and order structures on R in SIA? As far as the former is concerned, there is little difference from the classical situation: in SIA R is equipped with the usual addition and multiplication operations under which it is a field. In particular, R satisfies the condition that each x ≠ 0 has a multiplicative inverse. Notice, however, that since in SIA no microquantity (apart from 0 itself) is provably ≠ 0, microquantities are not required to have multiplicative inverses (a requirement which would lead to inconsistency). From a strictly algebraic standpoint, R in SIA differs from its classical counterpart only in being required to satisfy the principle of infinitesimal cancellation.
The situation is different, however, as regards the order structure of R in SIA. Because of the failure of the law of excluded middle, the order relation < on R in SIA cannot satisfy the trichotomy law
x < y ∨ y < x ∨ x = y,
and accordingly < must be a partial, rather than a total ordering. Since microquantities do not have multiplicative inverses, and R is a field, any microquantity ε must satisfy
¬ε < 0 ∧ ¬ε > 0.
Accordingly, if we define the relation < by x < y iff ¬(y < x), then, for any microquantity ε we have
ε ≤ 0 ∧ ε ≥ 0.
Using these ideas we can identify three infinitesimal neighbourhoods of 0 on R in SIA, each of which is included in its successor. First, the set Δ of microquantities itself, next, the set I = {x ∈ R : ¬x ≠ 0} of elements indistinguishable from 0; finally, the set J = {x ∈ R : x ≤ 0 ∧ x ≥ 0} of elements neither less nor greater than 0. These three may be thought of as the infinitesimal neighbourhoods of 0 defined algebraically, logically, and order-theoretically, respectively.
In certain models of SIA the system of natural numbers possesses some subtle and intriguing features which make it possible to introduce another type of infinitesimal—the so-called invertible infinitesimals—resembling those of nonstandard analysis, whose presence engenders yet another infinitesimal neighbourhood of 0 properly containing all those introduced above.
In SIA the set N of natural numbers can be defined to be the smallest subset of R which contains 0 and is closed under the operation of adding 1. In some models of SIA, R satisfies the Archimedean principle that every real number is majorized by a natural number. However, models of SIA have been constructed (see Moerdijk and Reyes [1991]) in which R is not Archimedean in this sense. In these models it is more natural to consider, in place of N, the set N* of smooth natural numbers defined by
N* = {x ∈ R: 0 ≤ x ∧ sin πx = 0}.
N* is the set of points of intersection of the smooth curve y = sin πx with the positive x-axis. In these models R can be shown to possess the Archimedean property provided that in the definition N is replaced by N*. In these models, then, N is a proper subset of N*: the members of N* − N may be considered nonstandard integers. Multiplicative inverses of nonstandard integers are infinitesimals, but, being themselves invertible, they are of a different type from the ones we have considered so far. It is quite easy to show that they, as well as the infinitesimals in J (and so also those in Δ and I) are all contained in the set—a further infinitesimal neighbourhood of 0—
K = {x ∈ R: ∀n ∈ N(−1/n+1 < x < 1/n+1)}
of infinitely small elements of R. The members of the set
In = {x ∈ K: x ≠ 0}
of invertible elements of K are naturally identified as invertible infinitesimals. Being obtained as inverses of “infinitely large” reals (i.e., reals r satisfying ∀n∈N(n < r) ∨ ∀n∈N(r < −n)) the members of In are the counterparts in SIA of the infinitesimals of nonstandard analysis.
Finally, a brief word on the models of SIA. These are the so-called smooth toposes, categories (see entry on category theory) of a certain kind in which all the usual mathematical operations can be performed but whose internal logic is intuitionistic and in which every map between spaces is smooth, that is, differentiable without limit. It is this “universal smoothness” that makes the presence of infinitesimal objects such as Δ possible. The construction of smooth toposes (see Moerdijk and Reyes [1991]) guarantees the consistency of SIA with intuitionistic logic. This is so despite the evident fact that SIA is not consistent with classical logic.
Bibliography
- Aristotle (1980). Physics, 2 volumes, trans. Cornford and Wickstead. Loeb Classical Library, Cambridge, MA: Harvard University Press and Heinemann.
- ––– (1996). Metaphysics, Oeconomica, Magna Moralia, 2 volumes, trans. Cooke and Tredinnick. Loeb Classical Library, Cambridge, MA: Harvard University Press.
- ––– (1996a). The Categories, On Interpretation, Prior Analytics, trans. Cooke and Tredinnick. Loeb Classical Library, Cambridge, MA: Harvard University Press.
- ––– (2000). On the Heavens, trans. Guthrie. Loeb Classical Library, Cambridge, MA: Harvard University Press.
- ––– (2000a). On Sophistical Refutations, On Coming-to-Be and Passing Away, On the Cosmos, trans. Forster and Furley. Loeb Classical Library, Cambridge, MA: Harvard University Press.
- Barnes, J. (1986).The Presocratic Philosophers, London: Routledge.
- Baron, M. E. (1987). The Origins of the Infinitesimal Calculus, New York: Dover.
- Beeson, M.J. (1985). Foundations of Constructive Mathematics, Berlin: Springer-Verlag.
- Bell, E. T. (ed.) (1945). The Development of Mathematics, 2nd, New York: McGraw-Hill.
- ––– (1965). Men of Mathematics, 2 volumes, London: Penguin Books.
- Bell, J. L. (1998). A Primer of Infinitesimal Analysis, Cambridge: Cambridge University Press.
- ––– (2000). “Hermann Weyl on intuition and the continuum,” Philosophia Mathematica, 8: 259–273.
- ––– (2001). “The continuum in smooth infinitesimal analysis,” in Schuster, Berger and Osswald (2001), pp. 19–24.
- ––– (2003). “Hermann Weyl’s later philosophical views: his divergence from Husserl,” in Husserl and the Sciences, R. Feist (ed.), Ottawa: University of Ottawa Press.
- ––– (2005) The Continuous and the Infinitesimal in Mathematics and Philosophy, Milan: Polimetrica S.A.
- Berkeley, G. (1960). Principles of Human Knowledge, New York: Doubleday.
- Bishop, E. (1967). Foundations of Constructive Analysis, New York: McGraw-Hill.
- Bishop, E., and D. Bridges (1985). Constructive Analysis, Berlin: Springer.
- Bolzano, B. (1950). Paradoxes of the Infinite, trans. Prihovsky, London: Routledge & Kegan Paul.
- Bos, H. (1974). “Differentials, higher order differentials and the derivative in the Leibnizian Calculus,” Archive for History of Exact Sciences, 14: 1–90.
- Boyer, C., (1959). The History of the Calculus and its Conceptual Development, New York: Dover.
- ––– (1968). A History of Mathematics, New York: Wiley.
- ––– and U. Merzbach (1989). A History of Mathematics, 2nd edition, New York: Wiley.
- Brentano, F. (1988). Philosophical Investigations on Space, Time and the Continuum trans. Smith, London: Croom Helm.
- Bridges, D. (1994). “A constructive look at the real line,” in Ehrlich (ed.) (1994), pp. 29–92.
- ––– (1999). “Constructive mathematics: a foundation for computable analysis,” Theoretical Computer Science, 219: 95–109.
- ––– and F. Richman (1987). Varieties of Constructive Mathematics, Cambridge: Cambridge University Press.
- Brouwer, L. E. J. (1975). Collected Works: 1. A. Heyting (ed.), Amsterdam: North-Holland.
- Burns, C. D. (1916). “William of Ockham on continuity,” Mind, 25: 506–12.
- Cajori, F. (1919). A Short History of the concepts of Limits and Fluxions, Chicago: Open Court.
- Cantor, G., (1961). Contributions to the Founding of the Theory of Transfinite Numbers, New York: Dover.
- Carnot, L. (1832). Reflexions sur la Métaphysique du Calcul Infinitesimal, trans. Browell, Oxford: Parker.
- Chevalier, G. et al. (1929). “Continu et Discontinu,” Cahiers de la Nouvelle Journée, 15: PAGES.
- Child, J. (1916) The Geometrical Lectures of Isaac Barrow, Chicago: Open Court.
- Cusanus, N. (1954). Of Learned Ignorance, trans. Heron, London: Routledge and Kegan Paul.
- D’ Alembert, J., and D. Diderot (1966). Encyclopédie, ou, Dictionnaire raisonné des sciences, des arts et des métiers / (mis en ordre et publié par Diderot, quant à la partie mathématique, par d'Alembert), Stuttgart: Cannstatt = Frommann.
- Dauben, J. (1979). Georg Cantor: His Mathematics and Philosophy of the Infinite, Cambridge, MA: Harvard University Press.
- Descartes, R. (1927). Discourse on Method, Meditations, and Principles of Philosophy (Everyman's Library), London: Dent.
- Dedekind, R. (1963). Essays on the Theory of Numbers, New York: Dover.
- Dugas, R. (1988). A History of Mechanics, New York: Dover.
- Dummett, M. (1977). Elements of Intuitionism, Oxford: Clarendon Press.
- Ehrlich, P., ed. (1994). Real Numbers, Generalizations of the Reals, and Theories of Continua, Dordrecht: Kluwer.
- Ehrlich, P. (1994a). All numbers great and small, in Ehrlich (ed.) (1994), pp. 239–258.
- Euler, L. (1843). Letters of Euler on Different Subjects in Natural Philosophy: Addressed to a German Princess; with Notes, and a Life of Euler, by David Brewster; Containing a Glossary of Scientific Term[s] with Additional Notes, by John Griscom, New York: Harper and Brothers.
- Euler, L. (1990). Introduction to Analysis of the Infinite, trans. Blanton, New York: Springer.
- Evans, M. (1955). “Aristotle, Newton, and the Theory of Continuous Magnitude,” Journal of the History of Ideas, 16: 548–557.
- Ewald, W. (1999). From Kant to Hilbert, A Source Book in the Foundations of Mathematics, Volumes I and II, Oxford: Oxford University Press.
- Fisher, G. (1978). “Cauchy and the Infinitely Small,” Historia Mathematica, 5: 313–331.
- ––– (1981), “The infinite and infinitesimal quantities of du Bois-Reymond and their reception,” Archive for History of Exact Sciences, 24/2: 101–163.
- ––– (1994) “Veronese's non-Archimedean linear continuum,” in Ehrlich (ed.) (1994), pp. 107–146.
- Folina, J. (1992). Poincaré and the Philosophy of Mathematics, New York: St. Martin's Press.
- Furley, D. (1967). Two Studies in the Greek Atomists. Princeton: Princeton University Press.
- ––– (1982). “The Greek commentators' treatment of Aristotle's theory of the continuous,” in Kretzmann (1982), pp. 17–36.
- ––– (1987). The Greek Cosmologists. Cambridge: Cambridge University Press.
- ––– and R. Allen (eds.) (1970). Studies in Presocratic Philosophy, Vol. I. London: Routledge and Kegan Paul.
- Galilei, G. (1954). Dialogues Concerning Two New Sciences, trans. Crew and De Salvio. New York: Dover.
- Gray, J. (1973). Ideas of Space: Euclidean, Non-Euclidean, and Relativistic, Oxford: Clarendon Press.
- Grant, E. (ed.) (1974). A Source Book in Medieval Science, Cambridge, MA: Harvard University Press
- Gregory, J. (1931). A Short History of Atomism, London: A. & C. Black.
- Grünbaum, A. (1967). Zeno's Paradoxes and Modern Science, London: Allen and Unwin.
- Hallett, M. (1984). Cantorian Set Theory and Limitation of Size, Oxford: Clarendon Press.
- Heath, T. (1949). Mathematics in Aristotle, Oxford: Oxford University Press.
- ––– (1981). A History of Greek Mathematics, 2 volumes, New York: Dover.
- Heyting, A. (1956). Intuitionism: An Introduction, Amsterdam: North-Holland.
- Hobson, E. W. (1957). The Theory of Functions of a Real Variable, New York: Dover.
- Hocking, J.G. and G. S. Young (1961). Topology, Reading, MA: Addison-Wesley.
- Houzel, C., et al. (1976). Philosophie et Calcul de l'Infini, Paris: Maspero.
- Hyland, J. (1979) “Continuity in spatial toposes,” in Fourman et al. (1979), pp. 442–465.
- Jesseph, D. (1993). Berkeley's Philosophy of Mathematics, Chicago: University of Chicago Press.
- Johnstone, P. T. (1977). Topos Theory, London: Academic Press.
- ––– (1982). Stone Spaces (Cambridge Studies in Advanced Mathematics, Volume 3), Cambridge: Cambridge University Press.
- ––– (1983). “The point of pointless topology,” Bull. Amer. Math. Soc. (New Series) 8 (1): 41–53.
- ––– (2002. Sketches of an Elephant: A Topos Theory Compendium, Vols. I and II (Oxford Logic Guides, Volumes 43 and 44), Oxford: Clarendon Press.
- Kahn, C. (2001). Pythagoras and the Pythagoreans: A Brief History, Indianapolis: Hackett.
- Kant, I. (1964). Critique of Pure Reason, London: Macmillan.
- ––– (1970). Metaphysical Foundations of natural Science, trans. Ellington, Indianapolis: Bobbs-Merrill.
- ––– (1977). Prolegomena to Any Future Metaphysics, trans. Carus, revised Ellington, Indianapolis: Hackett.
- ––– (1992). Theoretical Philosophy 1755–1770, Watford and Meerbote (eds.), Cambridge: Cambridge University Press.
- Keisler, H. (1994). “The hyperreal line,” in Ehrlich (ed.) (1994), pp. 207–238.
- Kirk, G. S., J. E. Raven, and M. Schofield (1983). The Presocratic Philosophers, 2nd edition, Cambridge: Cambridge University Press.
- Kline, M. (1972). Mathematical Thought from Ancient to Modern Times, 3 volumes, Oxford: Oxford University Press.
- Kock, A. (1981). Synthetic Differential Geometry, Cambridge: Cambridge University Press.
- Körner, S. (1955). Kant, Harmondsworth: Penguin Books.
- ––– (1960). The Philosophy of Mathematics, London: Hutchinson.
- Kretzmann, N., (ed.) (1982). Infinity and Continuity in Ancient and Medieval Thought, Ithaca: Cornell University Press.
- Lavendhomme, R. (1996). Basic Concepts of Synthetic Differential Geometry, Dordrecht: Kluwer.
- Lawvere, F. W. (1971). “Quantifiers and sheaves,” in Actes du Congrès Intern. Des Math. Nice 1970, tome I. Paris: Gauthier-Villars, pp. 329-34.
- ––– (1980). “Toward the description in a smooth topos of the dynamically possible motions and deformations of a continuous body,” Cahiers de Top. et Géom. Diff., 21: 377–92.
- Leibniz, G. (1951). Selections. Wiener (ed.), New York: Scribners.
- ––– (1961). Philosophical Writings, trans. Morris (Everyman Library), London: Dent.
- ––– (2001). The Labyrinth of the Continuum : Writings on the Continuum Problem, 1672–1686, trans. Arthur, New Haven: Yale University Press.
- Mac Lane, S. (1986). Mathematics: Form and Function, Berlin: Springer-Verlag.
- Mancosu, P. (1996). Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century, New York, Oxford: Oxford University Press.
- ––– (1998). From Brouwer to Hilbert: The Debate on the Foundations of Mathematics in the1920s, Oxford: Clarendon Press.
- McLarty, C. (1988). “Defining sets as sets of points of spaces,” J. Philosophical Logic, 17: 75–90.
- ––– (1992). Elementary Categories, Elementary Toposes, Oxford: Oxford University Press.
- Miller, F. (1982). “Aristotle against the atomists,” in Kretzmann (1982), pp. 87–111.
- Moerdijk, I. and Reyes, G. E. (1991). Models for Smooth Infinitesimal Analysis, Berlin: Springer-Verlag.
- Moore, A. W. (1990). The Infinite, London: Routledge.
- Murdoch, J. (1957). Geometry and the Continuum in the 14th Century: A Philosophical Analysis of Th. Bradwardinne's Tractatus de Continuo. Ph.D. Dissertation, University of Wisconsin.
- ––– (1982). “William of Ockham and the logic of infinity and continuity,” in Kretzmann (1982), pp. 165–206.
- Newton, I. (1730). Opticks, New York: Dover, 1952.
- Newton, I., (1962). Principia, Vols, I, II, trans. Motte, revised. Cajori, Berkeley: University of California Press.
- Nicholas of Autrecourt (1971). The Universal Treatise, trans. Kennedy et al., Milwaukee: Marquette University Press.
- Peirce, C.S. (1976). The New Elements of Mathematics, Volume III, Carolyn Eisele (ed.), The Hague: Mouton Publishers and Humanities Press.
- ––– (1992). Reasoning and the Logic of Things, Kenneth Laine Ketner (ed.), Cambridge, MA: Harvard University Press.
- Peters, F. (1967), Greek Philosophical Terms, New York: New York University Press.
- Poincaré. H. (1946). Foundations of Science, trans. G. Halsted, New York: Science Press.
- ––– (1963). Mathematics and Science: Last Essays, New York: Dover.
- Pycior, H. (1987). “Mathematics and Philosophy: Wallis, Hobbes, Barrow, and Berkeley.” Journal of the History of Ideas, 48 (2): 265–286.
- Pyle, A. (1997). Atomism and Its Critics, London: Thoemmes Press.
- Rescher, N. (1967). The Philosophy of Leibniz, Upper Saddle River: Prentice-Hall.
- Robinson, A. (1996). Non-Standard Analysis, Princeton: Princeton University Press.
- Russell, B. (1958). A Critical Exposition of the Philosophy of Leibniz, 2nd edition, London: Allen & Unwin.
- Sambursky, S. (1963). The Physical World of the Greeks, London: Routledge and Kegan Paul.
- ––– (1971). Physics of the Stoics, London: Hutchinson.
- Schuster, P., U. Berger and H. Osswald (2001). Reuniting the Antipodes—Constructive and Nonstandard Views of the Continuum, Dordrecht: Kluwer.
- Sorabji, R. (1982). “Atoms and time atoms,” in Kretzmann (1982), pp. 37–86.
- ––– (1983). Time, Creation and the Continuum, Ithaca: Cornell University Press.
- Stokes, M. (1971). One and Many in Presocratic Philosophy, Cambridge, MA: Harvard University Press.
- Stones, G.B. (1928). “The atomic view of matter in the XVth, XVIth and XVIIth centuries,” Isis, 10: 444–65.
- Struik, D. (1948). A Concise History of Mathematics, New York: Dover
- Truesdell, C. (1972). Leonard Euler, Supreme Geometer. In Irrationalism in the Eighteenth Century, H. Pagliaro (ed.), Cleveland: Case Western Reserve University Press.
- Van Atten, M., D. van Dalen and R. Tieszen (2002). “The phenomenology and mathematics of the intuitive continuum,” Philosophia Mathematica, 10: 203–236.
- Van Cleve, J. (1981). “Reflections on Kant's 2nd antinomy,” Synthese, 47: 1147–50.
- Van Dalen, D. (1995). “Hermann Weyl's intuitionistic mathematics,” Bulletin of Symbolic Logic, 1 (2): 145–169.
- ––– (1997). “How connected is the intuitionistic continuum?,” Journal of Symbolic Logic, 62: 1147–50.
- ––– (1998). “From a Brouwerian point of view,” Philosophia Mathematica, 6: 209–226.
- Van Melsen, A. (1952). From Atomos to Atom, trans. Koren, Pittsburgh: Duquesne University Press.
- Vesley, R. (1981). An Intuitionistic Infinitesimal Calculus (Lecture Notes in Mathematics: 873), Berlin: Springer-Verlag, pp. 208–212.
- Wagon, S. (1993). The Banach-Tarski Paradox, Cambridge: Cambridge University Press.
- Weyl, H. (1929). Consistency in Mathematics, Pamphlet 16, Houston: Rice Institute Pamphlets, pp. 245–265. Reprinted in Weyl (1968) II, pp. 150–170.
- ––– (1932). The Open World: Three Lectures on the Metaphysical Implications of Science, New Haven: Yale University Press.
- ––– (1940). “The ghost of modality,” Philosophical Essays in Memory of Edmund Husserl, Cambridge, MA: Harvard University Press. Reprinted in Weyl (1968) III, pp. 684–709.
- ––– (1949). Philosophy of Mathematics and Natural Science, Princeton: Princeton University Press.
- ––– (1950). Space-Time-Matter, trans. Brose, New York: Dover. (English translation of Raum, Zeit, Materie, Berlin: Springer Verlag, 1921.)
- ––– (1954). “Address on the unity of knowledge,” Columbia University Bicentennial Celebration. Reprinted in Weyl (1968) IV, pp. 623–630.
- ––– (1968). Gesammelte Abhandlungen, I-IV, K. Chandrasehharan (ed.), Berlin: Springer-Verlag.
- ––– (1969). “Insight and reflection,” Lecture delivered at the University of Lausanne, Switzerland, May 1954. Translated from German original in Studia Philosophica 15, 1955. In T.L. Saaty and F.J. Weyl (eds.), The Spirit and Uses of the Mathematical Sciences, pp. 281–301. New York: McGraw-Hill, 1969.
- ––– (1985). “Axiomatic versus constructive procedures in mathematics,” T. Tonietti (ed.), Mathematical Intelligencer, 7 (4): 10–17, 38.
- ––– (1987). The Continuum: A Critical Examination of the Foundation of Analysis, trans. S. Pollard and T. Bole, Philadelphia: Thomas Jefferson University Press. (English translation of Das Kontinuum, Leipzig: Veit, 1918.)
- ––– (1998). “On the New Foundational Crisis in Mathematics,” in Mancosu (1998), pp. 86–122. (English translation of ‘Über der neue Grundlagenkrise der Mathematik,’ Mathematische Zeitschrift 10, 1921, pp. 37–79.)
- ––– (1998a). “On the Current Epistemological Situation in Mathematics,” in Mancosu (1998), pp. 123–142. (English translation of ‘Die heutige Erkenntnislage in der Mathematik, Symposion 1, 1925–27, pp. 1–32.)
- White, M. J. (1992). The Continuous and the Discrete: Ancient Physical Theories from a Contemporary Perspective, Oxford: Clarendon Press, Oxford.
- Whyte, L. (1961). Essay on Atomism from Peano to 1960, Middletown, CT: Wesleyan University Press.
- Wike, V. (1982). Kant's Antinomies of Reason: Their Origin and Resolution, Lanham, MD: University Press of America.
Other Internet Resources
- Lawvere, F.W. (1998). “Outline of synthetic differential geometry”, unpublished manuscript.
Related Entries
Aristotle | Berkeley, George | Bolzano, Bernard | Brentano, Franz | Brouwer, Luitzen Egbertus Jan | category theory | change | Cusanus, Nicolaus [Nicolas of Cusa] | Democritus | Descartes, René | Duns Scotus, John | Epicurus | Galileo Galilei | geometry: finitism in | Kant, Immanuel | Kepler, Johannes | Leibniz, Gottfried Wilhelm | Leucippus | logic: intuitionistic | mathematics: constructive | Newton, Isaac | Ockham [Occam], William | Peirce, Charles Sanders | Zeno of Elea: Zeno's paradoxes
Acknowledgments
For a comprehensive account of the evolution of the concepts of continuity and the infinitesimal, see Bell (2005), on which the present article is based.