Natural Selection
Darwin's theory of evolution by natural selection provided the first, and only, causal-mechanistic account of the existence of adaptations in nature. As such, it provided the first, and only, scientific alternative to the “argument from design”. That alone would account for its philosophical significance. But the theory also raises other philosophical questions not encountered in the study of the theories of physics. Unfortunately the concept of natural selection is intimately intertwined with the other basic concepts of evolutionary theory—such as the concepts of fitness and adaptation—that are themselves philosophically controversial. Fortunately we can make considerable headway in getting clear on natural selection without solving all of those outstanding problems.
- 1. Natural Selection and Evolutionary Theory
- 2. Natural Selection and Fitness
- 3. Common Selective Environments
- 4. Does Natural Selection Require Differential Reproduction?
- 5. Does Natural Selection Require Heritable Variation?
- 6. Natural Selection and Drift
- 7. Bibliography
- Other Internet Resources
- Related Entries
1. Natural Selection and Evolutionary Theory
The theory of evolution by natural selection forms a central part of modern evolutionary theory. There is some controversy among biologists as to just how important natural selection is compared to other processes producing evolutionary change, but there is no controversy over the proposition that natural selection is important. Some good might come of the efforts to produce a general selection theory that would include the natural selection that occurs as a part of the evolutionary process as a special case (e.g. Hull 2001), but here the focus will be solely on the evolutionary process.
Biology starts when reproduction begins. Stars may be said to evolve, but they do not reproduce and so biological theory does not apply to them. Biological evolution requires reproducing entities that form lineages. It is these lineages that evolve. Thus it is only within such lineages that we will properly apply the term natural selection. A kindergarten class may certainly select among different colored candies, but since those candies are not part of self-reproducing lineages, we should not confuse this selection process with natural selection.
2. Natural Selection and Fitness
Natural selection is a causal process. Distinguishing it from other processes in evolution is one of major conceptual and empirical problems of evolutionary biology. The bare bones of Darwin's theory of evolution by natural selection are elegantly simple. Typically (but not necessarily) there is variation among organisms within a reproducing population. Oftentimes (but not always) this variation is (to some degree) heritable. When this variation is causally connected to differential ability to survive and reproduce, differential reproduction will probably ensue. This last claim is one way of stating the Principle of Natural Selection (from here on PNS). The PNS goes beyond the causally neutral statement that is sometimes listed as the third of what are often called “Darwin's Three Conditions”, viz., different variants sometimes reproduce at different rates. That statement leaves open the question of whether or not the variation in question is causally responsible for the differential reproduction. It leaves open the question of whether a qualitatively similar outcome would result from repeated iterations of this set-up. It leaves open the question of whether this process is natural selection or drift (see below). It—the causally neutral statement—does not suffice to state Darwin's causal theory. Darwin clearly recognized this (see, for example 1871) as did Lewontin (1978); although many contemporary commentators fail to see this.
Why is it that some variants leave more offspring than others? In those cases we label natural selection, it is because those variants are better adapted, or are fitter than their competitors. Thus we can define natural selection as follows: Natural selection is differential reproduction due to differential fitness (or differential adaptedness) within a common selective environment (see next section). This definition makes the concept of natural selection dependent on that of fitness, which is unfortunate since many philosophers find the concept of fitness deeply mysterious (see e.g., Ariew and Lewontin 2004). But like it or not, that is the way the theory is structured. And, fortunately, we can make considerable headway in understanding natural selection without solving all of the philosophical problems surrounding the concept of fitness.
3. Common Selective Environments
As a causal theory natural selection locates the causally relevant differences that lead to differential reproduction. These differences are differences in organisms' fitness to their environment. Or, more fully, they are differences in various organismic capacities to survive and reproduce in their environment. When these differences in capacities are heritable, then evolution will (usually) ensue. This sort of case must be carefully distinguished from cases where the causes of differential reproduction are not located in the organisms, but rather in their different environments. Let us make this distinction more concrete. Imagine two genotypes of an annual plant that grows in dense patches. Sunlight is at a premium and taller plants shade shorter plants thus garnering more energy for growth and reproduction. One genotype, G1, grows more quickly at germination than the other, G2. Thus G1s are initially taller than G2s and this difference persists throughout the growing season due to G1s increased energy stores. The consequence of this is that G1s produce more flowers, more pollen and more seeds than G2s. This is natural selection at work.
In contrast, imagine two genotypes of the same species, G3 and G4 that do not differ in germination date, growth rate, resource allocation between growth and reproduction or any other factor relevant to reproduction when grown in a common environment. Now imagine that seeds of these two genotypes are distributed randomly across a patchwork of two quite different soil types, call them E1 and E2. E1 and E2 are identical except that E1 contains high levels of lead whereas E2 does not. Lead dramatically and equally reduces growth and reproduction in both G3 and G4. Finally imagine that this random distribution process results in a correlation between genotype and environment—i.e., G3s are disproportionately found in E1. In consequence of all of this, G4s produce more flowers, more pollen and more seeds than G3s. But natural selection is not occurring here. (Indeed this is a type of drift, see below.)
In both cases differential reproduction occurs, and in both cases I have already sketched causal explanations of this. In neither case is differential reproduction mysterious (although chance does play a role in the second explanation, but not the first). But only the first case could result in adaptive evolution. (See Brandon 1990, chapter 2 for fuller discussion.) Biologists have long recognized the importance of the difference discussed above, thus the importance of so-called “common garden” experiments in experimental evolutionary genetics. (In common garden experiments, the environments in which different genotypes are placed are controlled as far as possible. Furthermore, when environmental control is imperfect, statistical techniques, in particular the analysis of variances and covariances, are employed to separate out the effects of genotype vs. environment.)
Clearly the two cases sketched above are highly simplified, and it might be objected that nature is unlikely to contain many examples that either model exactly applies to. This objection has both epistemological and ontological sides. The epistemological side of the objection has, I think, been met. First, the statistical techniques mentioned in the last paragraph mitigate the force of it. Even in messy cases biologists are fairly successful in separating out environmental causes from genetic, or organismic, causes of differential reproduction. (It should at least be mentioned here that this sort of analysis also often yields genotype by environment interactions, G × E. This occurs when, in contrast to case 2, the relative performance of different genotypes differs in different environments. Although common in nature, and very important, we can ignore that here.) Second, the experimental techniques and conceptual resources developed by Antonovics et al. (1988), Brandon (1990) and Brandon and Antonovics (1996) allow for precise measurements of environmental heterogeneity in real life populations.
Ontologically the objection is this: when measured precisely enough each organism lives in a unique environment. Thus if natural selection requires multiple organisms competing in a common selective environment, then it never really occurs. That, if true, would be a serious objection to the picture of natural selection I am presenting here. But I think we have very good reason to believe it is not true. Unfortunately, here I can present only the briefest sketch of it. What natural selection explanations require is consistent ordinal relations in fitness of the competing types—they do not require precise agreement of absolute fitnesses of the competing types. Lots of empirical studies of natural selection in the wild have shown consistent ordinal fitness relations (see Endler 1986). Furthermore, the fact of adaptive evolution, the consistent and persistent increase of one type over others in evolutionary history, requires these consistent ordinal relations, or what I have termed “common selective neighborhoods”. Thus I think the ontological objection has been met as well.
4. Does Natural Selection Require Differential Reproduction?
The short answer to this question is “Yes”. I have already offered arguments in favor of that answer. However the longer more complete answer is “No, no, but yes”. I will explain.
There are two reasonable arguments that suggest a negative answer to our question. I will review them both. In the beginning of this essay I stated that considerable progress could be made in articulating a clear and adequate conception of natural selection without solving all of the philosophical problems associated with the notion of fitness. However, in this section I will have to make certain assumptions about fitness in order to address the issues to be raised. The assumptions are quite plausible, but not defensible in a short essay of this sort.
One negative answer is based on a radical rethinking of the problem nature presents to evolving entities. Mainstream evolutionary biology measures fitness in terms of reproductive success. (Exactly how it defines fitness will not be addressed here.) Survival is important exactly insofar as it contributes to reproduction. Evolutionary success is reproductive success. But suppose we turn the relation between reproduction and survival on its head and think of reproduction as important only insofar as it contributes to lineage survival. The fundamental evolutionary problem is persistence, and reproduction is but one means of achieving that (Bouchard 2004). Compare two lineages, one composed of short-lived organisms that reproduce every year, the other composed of organisms that live for 1,000+ years, but reproduce only rarely. At the end of a thousand year period the first may have gone extinct, while the second persists in virtue of simply surviving without reproduction. Isn't this radical view just as defensible as the more mainstream view? If so, then differential persistence would count as natural selection, and differential reproduction would not be necessary for natural selection to occur.
Interesting as this view is, I reject it because, with Dawkins (1982), I believe that reproduction, in particular going through a single cell bottle neck from whence the developmental process is started anew, is necessary for the evolutionary process of adaptation. Only by restarting the developmental process each generation can fundamental alterations of that process be achieved. Consider a grove of aspens that grows vertically (in what we intuitively think of as trees) and horizontally by underground runners that produce more “trees”. The phenotype of the whole grove can change through time—growing vigorously here, not growing there. But consider a genetic mutation that would fundamentally alter Aspen phenotype. It may occur in a multicellular runner. If so, it will be incorporated in the resultant cell lineage. But that cell lineage will be one of many in the next “tree” produced, since the next tree grows not from a single cell, but from a multi-cell runner. Thus the resultant “tree” will be a chimera, and not fundamentally different from the others in the grove. In contrast, were the runners single-celled at any cross-section, then a somatic mutation would be incorporated in the whole of the downstream “tree”. This, according to Harper (1977) and Dawkins (1982), would count as reproduction, not growth, because this could fundamentally rearrange Aspen development. (But that is not the way Aspens grow.) Accordingly, the evolution of complex adaptations, fundamental rearrangements of development, requires differential reproduction.
A second reason to answer our question in the negative comes from a (quite appropriate) focus on the ecological process of selection. For practical reasons, many studies of natural selection in the wild focus on only a small part of the life cycle. For instance, in the most famous such study H. B. D. Kettlewell (1955, 1956) marked different morphs of the peppered moth, Biston betularia, released them (into polluted woods in one treatment, non-polluted woods in another) and then recaptured them three days later. The difference in the proportion of dark to light forms in the recaptured vs. the released groups was taken to measure natural selection in action. As Rudge (1999) points out, Kettlewell had preformed numerous auxiliary studies to justify this inference, but for present concerns what is crucial is that Kettlewell looked at only a small portion of the entire life cycle, and in particular a portion that did not involve reproduction. It is beyond the scope of this essay to critically examine Kettlewell's actual work, but let us use it as a basis to construct two hypothetical examples.
The first example mirrors the situation with which Kettlewell was actually dealing. Let us suppose that there are two genetically distinct morphs in a population of moths, call them Light and Dark. In survivorship through the larval stage both forms are identical. They are also identical in fertility and fecundity. They differ only in survivorship during the adult stage prior to mating. This difference is due to a difference in their conspicuousness to birds as they rest on the trunks of trees. On dark trees the Darks are less conspicuous than Lights, and vice versa on light trees. In a polluted wood, most of the tree trunks are dark. A biologist marks equal numbers of Darks and Lights, releases them into the polluted woods and recaptures them three days later. She recaptures twice as many Darks as Lights. Based on her knowledge of when pollution was introduced into the woods, the frequency of the two morphs in woods that have not been polluted, the underlying genetics of the two morphs, and her observed selection differential between them, she builds a population genetic model of the situation that predicts a relative frequency of the two morphs for the present. That prediction fits the observed frequencies. She concludes that her mark-release-recapture experiment has captured natural selection in action. I, and the vast majority of evolutionary biologists, would agree with this conclusion.
In contrast, imagine a second example. It is just like the first except that in the larval stage the Lights out survive the Darks by a two to one margin. This difference in survival in the larval stage exactly counterbalances the difference in survival in the adult stage, leading to no difference in reproductive success between the two morphs. Were this going on we couldn't explain the match between frequencies observed in different woods and the selective processes occurring in the adult stage. But that is not crucial to our question. The question for us is: Are the two processes observed in the mark-release-recapture studies in our hypothetical cases both examples of natural selection?
If you think, as has been suggested, that natural selection requires differential reproduction, then you must say that the second example is not one of natural selection. But one might object to this conclusion as follows. The ecological process of birds preying on moths based on their relative conspicuousness is exactly the same in the two examples. That ecological process was identified as natural selection in the first example; therefore it must be natural selection in the second example as well.
Although quite compelling I think the above should be resisted in the following way. Fitness attaches to the whole life cycle, not some subpart of it. Why? Again the short answer relies on a commitment to the fundamentality of reproduction. Reproduction is a reproduction of the entire life cycle. It is true that fitness is often measured, as in Kettlewell's case or in our hypothetical examples, by looking at only a part of the life cycle. But from an evolutionary point of view we are interested in this only when relative performance in this part of the life cycle actually influences relative reproductive success. Thus the first, but not the second, is a case of natural selection. (Consider how Kettlewell's studies would have been received by the evolutionary community if they had mirrored our second hypothetical example rather than the first.)
And so natural selection does require differential reproduction.
5. Does Natural Selection Require Heritable Variation?
In the preceding section we had to draw some fairly subtle distinctions, but our conclusion is one with which the vast majority of evolutionary biologists would agree. There is no such answer to the question of this section. Many biologists define natural selection as differential reproduction of heritable variation (see, e.g., Endler 1986). Many other biologists follow the tradition of quantitative genetics and draw a sharp distinction between the ecological process of selection and the evolutionary response to selection (see e.g., Falconer 1981). There are a large number of advantages to the second approach, and I will follow it here. Thus we will arrive at a negative answer to the question of this section.
First we must get clear on the relevant sense of heritability. Recall § 2 above where we stated “Darwin's Three Conditions”. They are: variation; heredity; and differential reproduction. The notion of heritability relevant here is the purely phenotypic, purely statistical notion developed by Francis Galton (1869). That notion identifies heritability with the regression of the offspring phenotype on the parental (or biparental mean in the case of sexual reproduction), where both phenotypes are presented as z-scores (i.e., set to mean = 0 and standard deviation = 1). Intuitively the heritability is a measure of how closely offspring deviation from the (offspring) mean phenotypic value matches that of the parental deviation (from the parental mean). That is, it measures the degree to which, for example, taller than average parents produce taller than average offspring. A value of 1 represents a perfect correlation between offspring and parental deviations from their respective means, while a value of 0 means there is no correlation, so that, for example, the offspring of tall parents would not differ statistically from those of short.
Unfortunately many people think that some sort of genetic definition has supplanted this basic concept of heritability. In particular, many would say that the Galtonian notion corresponds to the “narrow sense” of heritability (h2), h2 = VA/VT , where VA is the additive genetic variance and VT is the total variance. (VT is usually decomposed into VA, VD—the variance due to allelic dominance, and Ve—the environmental variance. The latter is in fact a statistical catch-all, so it includes not just variation due to environmental differences, but everything else.) Even though this equation is very important and we will revert to it shortly, we cannot accept this as a definition of heritability for at least two reasons: (1) Even for diploid sexually reproducing organisms that equation holds only under certain genetic conditions (Roughgarten 1979); and (2) It certainly is not applicable to pre-genetic or non-genetic systems. But that would mean that the theory of evolution by natural selection would not be applicable to the early stages of life on this planet, nor to epigenetic inheritance, nor to cultural transmission, nor to life elsewhere in the universe. Surely such consequences are unacceptable and entirely unnecessary. Thus the Galtonian notion of heritability is fundamental.
The motivation for saying that natural selection requires heritable variation is clear. Only selection acting on heritable variation will have evolutionary consequences. And since we are interested in the concept of natural selection from a purely evolutionary point of view (recall the introduction to this piece), we don't count selection acting on non-heritable variation as natural selection. (This seems analogous to the argument in the last section saying that selection acting in a part of the life cycle that is exactly counterbalanced later in the life cycle should not count as natural selection.)
One response to this line of reasoning is to insist on the importance of drawing a sharp distinction between the ecological process of selection and the evolutionary process of response to selection. The ecological process of selection, the domain of ecological genetics, is complicated and difficult to study. The evolutionary response to selection is the domain of population genetics. It too is complicated and difficult. From a purely strategic point of view it would seem wise not to conflate these two complex processes into one.
I think most would agree with this bit of wisdom, but some would counter by saying that it does not require a definition of natural selection that is neutral on the heritability of the variation in question. We can define ‘natural selection’ one way or another and still agree on all of the facts. The argument for one definition over the other will have to be made in terms of simplicity, elegance, or some other non-empirical virtue of theoretical constructs.
Let us illustrate the last point with a simple example, an example that has been commonly used in the philosophical literature on units of selection. The example is of heterozygote superiority, though any example where the allelic effects on phenotype are non-additive would do. (As would any number of cases involving non-additive interactions among multiple genes.) There are two alleles at a locus, A and a, and thus three genotypes, AA, Aa, and aa. For simplicity suppose that the two homozygotes are lethal, i.e., they die before reproducing. Thus all the matings are Aa x Aa. Mendelism results in offspring of genotypes AA, Aa and aa, in the ratio of 1:2:1. In a single generation the allele frequencies equilibrate at 50:50 and stay there unless the fates of homozygotes changes.
Although we criticized the genetic “definition” of heritability as being derived and not general; it is useful for simple genetic models like the one just described. In this example, once the stable equilibrium is reached, the heritability, h2, is zero. This is true because the additive genetic variation is zero. (To apply the Galtonian notion of heritability to this example, we would need to complicate it by specifying a genotype-phenotype mapping, since that notion relates phenotypes. We could do this, and provided Ve is not zero the Galtonian value would be zero. But the point presently under discussion would not be made stronger by this extra complication.) So here we have a case where there is phenotypic variation caused by genotypic variation, but the heritability of this variation is zero because of the non-linear relationship between genotype and fitness. How do we categorize the differential reproduction that occurs in this example? Those who think that natural selection requires the differential reproduction of heritable variation would say there is no natural selection here. Those following the quantitative genetics tradition would say that natural selection is occurring, but that since h2 is zero the response to selection is zero. (In accordance with the fundamental formula of quantitative genetics, R = h2S, where R is the response to selection and S is the selection differential.) But, it seems, there is no empirical difference between these two points of view, so we need to decide between them on the basis of some non-empirical reasons.
The seeming empirical equivalence between the two accounts offered of our example is, in fact, illusory. Godfrey-Smith and Lewontin (1993) have pointed out that there is an empirical difference between an account of this case that says there is selection vs. one that says there is no selection. (They make this point in the context of discussing genic selectionism, which is committed to saying that there is no selection in this case since the allelic fitnesses are the same. For further discussion of this see Brandon and Nijhout 2006.) The empirical difference is that the first, but not the second, can account for the within generation change in genotype frequencies. At the start of each generation the three genotypes are represented in the 1:2:1 ratio discussed above. Later in the generation the homozygotes, both AA and aa, die, so that 100% of the population is composed of Aas. However, this difference is not an evolutionary difference, since evolution is trans-generational change. Our focus is on evolution. And it turns out that the two models are not empirically equivalent with respect to evolutionary predictions. The standard account, which says that selection occurs each generation against the homozygotes, predicts a stable equilibrium—one actively maintained by strong selection. But the account that says that there is no selection in this case has no basis to predict the same sort of stable equilibrium. This is not apparent if one only considers selection, because the genic selectionist recognizes the existence of selection once one perturbs the population from its equilibrium and so, it would seem, both models predict the same stable equilibrium. However, once one brings in considerations of the interaction of drift and selection (see next section) it has been shown that the models do not give empirically equivalent predictions (Brandon and Nijhout 2006). This is because small perturbations from equilibrium will have very different likelihoods of drift, because they will experience quantitatively quite different regions within which drift vs. selection is likely to dominate.
This example has a number of consequences (again see Brandon and Nijhout 2006 and Brandon 2006). But for us the consequence is this. To say that selection requires heritable variation is factually wrong. When applied to a broad class of cases it makes the wrong evolutionary predictions. And so we must reject that view, and conclude that natural selection does not require heritable variation.
6. Natural Selection and Drift
Why should an entry on natural selection contain a section on drift? One good reason is that natural selection and drift are co-products of the same process, namely a probabilistic sampling process (Brandon and Carson 1996, Matthen and Ariew 2002, Walsh et al. 2002). Thus, although it is of crucial importance to separate selection and drift, one cannot do so on the basis of process alone (contra Millstein 2002), one must do so on the basis on outcomes (Brandon 2005). Why is this? If we think of fitness as a probabilistic propensity, then, as we have seen, differential fitness is a necessary condition for natural selection. Thought of this way, natural selection is a probabilistic sampling process. We can characterize a continuum of all possible fitness differences starting with maximal fitness differences at one end of the continuum (i.e. where all fitness equal either 1 or 0, with at least some of each value), and minimum fitness differences on the other (i.e., an equiprobable distribution). The two endpoints are exceptional with respect to the relation of selection and drift. At the maximal fitness difference end, one unlikely to occur in nature, drift is impossible and selection is necessary. (See Figure 1.) At the finite set of minimal fitness differences at the other end of the continuum, corresponding to absolute neutrality of the traits under consideration, selection is impossible, because there are no fitness differences. And drift is maximally likely, but not necessary. Why not? Because the sample may be in accord with the probabilistic expectations and thus no drift occur. (Imagine a population with two alleles, A and a, absolutely selectively neutral with respect to each other, and at a 50:50 ratio. The next generation may also contain the two alleles at the same ratio, if so, no drift has occurred.
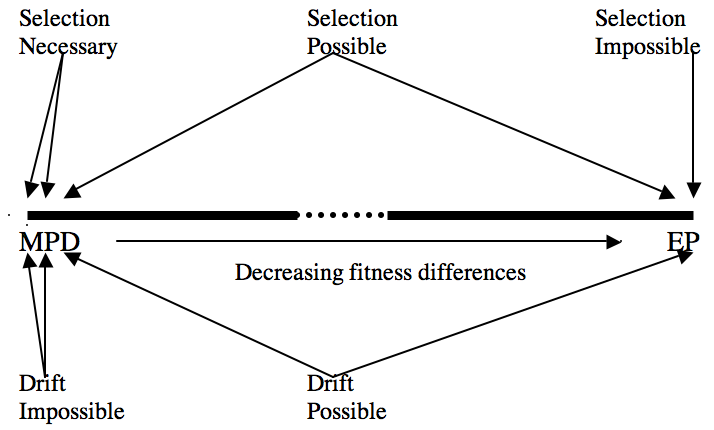
Figure 1. The heavy horizontal line, with dotted center section, represents the infinite number of possible fitness distributions from Maximal Probability Differences (MPD—all fitness = 0 or = 1, with some of both) on the left to the Equiprobable Distribution (EP—all fitness the same) on the right. The arrows emanating from the different descriptions of the modalities of selection and drift indicate the areas of the distribution falling under these descriptions.
But these two endpoints of this continuum are exceptional. More common is surely the vast middle area where drift and selection are both possible. In this middle ground we cannot say until after the fact whether or not drift occurs, nor quantify the degree to which it occurs. Prior to the fact we can only quantify the relative likelihoods of selection and drift—they vary according to the crucial quantity 4Ns. (Where N is the effective population size and s is the selection coefficient, i.e. the strength of selection. For discussion of 4Ns see any standard textbook on population genetics, e.g., Roughgarden 1979, see also Brandon and Nijhout, 2006.) The larger that quantity is, the larger N and the larger s, the greater is the likelihood that selection will dominate drift. And vice versa for small N and small s. Only after the fact can one tell whether or not the probabilistic sampling has gone in accord with the probabilistic expectations, or not. To the extent that it has not, drift has occurred. Drift simply is the deviation from probabilistic expectation. And since selection itself is a probabilistic process there can be no purely process-derived distinction between selection and drift—attractive as that idea may be.
A more fundamental reason for a discussion of drift here in an entry on natural selection is the view that drift is the zero-force background against which evolutionary forces, including natural selection, act (Brandon 2006). Just as in Newtonian mechanics one could not properly understand the notion of gravitational force, without understanding Newton's 1st Law, similarly one cannot understand natural selection in evolutionary biology without understanding the background against which it operates. Put in other terms, drift provides the appropriate null hypothesis against which to test any selection hypothesis. Unfortunately this is not always well understood. Indeed this way of thinking about evolution stands some canonical versions of evolutionary theory on their heads. For instance, those who would take the Hardy-Weinberg Law as a Zero-Force Law of evolution (see, e.g., Ruse 1973, and Sober 1984, but also many standard textbooks in evolution) view stasis as the default state of evolutionary systems, with some evolutionary force needed to move (i.e. evolve) them. Without a net force, no net change. But all modern methodology in molecular evolution is predicated of the truth of just the opposite idea, namely that left alone evolutionary systems drift. Drift is the default state. So that, for instance, neutral alleles in different populations differentiate from each other. But this molecular truth is iterated throughout the biological hierarchy. Once speciation occurs, species differentiate (drift apart) as a null expectation. Which is not to say that natural selection cannot produce evolutionary change. Of course it can. But if we are to properly recognize it, we must be able to recognize the signature of selection and differentiate it from drift's signature (see, e.g., Bamshad and Wooding 2003). Change in evolution is a heterogeneous category.
Stasis, on the other hand, is largely homogeneous. Long-term stasis can only occur by natural selection.
7. Bibliography
- Antonovics, J., Ellstrand, N. C., and Brandon, R. N., 1988, “Genetic variation and environmental variation: Expectations and experiments,” in Plant Evolutionary Biology, (eds.) L. D. Gottlieb and S. K. Jain, pp. 275–303. London: Chapman and Hall.
- Ariew, A. and Lewontin, R. C., 2004, “Confusions of fitness,” British Journal for the Philosophy of Science 55: 347–363.
- Bamshad, M. and Wooding, S. P., 2003, “Signatures of natural selection in the human genome,” Nature Review Genetics 4: 99–111.
- Bouchard, F., 2004, Evolution, Fitness and the Struggle for Persistence, Ph. D. dissertation, Duke University.
- Brandon, R. N., 1990, Adaptation and Environment, Princeton: Princeton University Press.
- Brandon, R. N., 2005, “The difference between selection and drift: A reply to Millstein,” Biology and Philosophy 20: 153–170.
- Brandon, R. N., 2006, “The principle of drift: Biology's first law,” Journal of Philosophy 103(7): 319–335.
- Brandon, R. N., and Antonovics, J., 1996, “The coevolution of organism and environment,” in Concepts and Methods in Evolutionary Biology, R. N. Brandon, pp. 161–178. Cambridge: Cambridge University Press.
- Brandon, R. N., and Carson, S. 1996, “The indeterministic character of evolutionary theory: no ‘no hidden variable proof’ but no room for determinism either,” Philosophy of Science 63: 315–337.
- Brandon, R. N. , and Nijhout, H. F. 2006, “The empirical non-equivalence of genic and genotypic models of selection: a (decisive) refutation of genic selectionism and pluralistic genic selectionism, ” Philosophy of Science 73: 277–297.
- Darwin, C., 1871, The Descent of Man, London: John Murray.
- Dawkins, R., 1982, The Extended Phenotype, Oxford: Freeman.
- Endler, J. A., 1986, Natural Selection in the Wild, Princeton: Princeton University Press.
- Falconer, D. S., 1981, Introduction to Quantitative Genetics, New York: Springer-Verlag.
- Galton, F., 1869. Hereditary Genius, London: Macmillan and Co.
- Godfrey-Smith, P., and Lewontin, R. C., 1993, “The dimensions of selection,” Philosophy of Science 60: 373–395.
- Harper, J. L., 1977. The Population Biology of Plants, London: Academic Press.
- Hull D. L., 2001, Science and Selection, Cambridge: Cambridge University Press.
- Kettlewell, H. B. D., 1955, “Selection experiments on industrial melanism in the Lepidoptera,” Heredity 9: 323–342.
- Kettlewell, H. B. D., 1956, “Further selection experiments on industrial melanism in the Lepidoptera,” Heredity 10: 287–301.
- Lewontin, R. C., 1978, “Adaptation,” Scientific American 239 (9): 156–169.
- Matthen, M. and Ariew, A. 2002, “Two ways of thinking about natural selection,” Journal of Philosophy 49(2): 55–83.
- Millstein R. L. 2002, “Are Random Drift and Natural Selection Conceptually Distinct?” Biology and Philosophy 17: 33–53.
- Roughgarden, J. 1979, Theory of Population Genetics and Evolutionary Ecology: An Introduction. New York: Macmillan Publishing Company, (Reprinted 1987 by Macmillan, and in 1996 by Prentice Hall).
- Rudge, D. W., 1999, “Taking the peppered moth with a grain of salt,” Biology and Philosophy 14: 9–37.
- Ruse, M., 1973, The Philosophy of Biology, London: Hutchinson Publishing Group, (Reprinted 1998 by Prometheus Books).
- Sober, E., 2004, The Nature of Selection: Evolutionary Theory in Philosophical Focus, Cambridge: MIT Press.
- Walsh, D., Lewens, T. and Ariew, A., 2002, “Trials of life: natural selection and random drift,” Philosophy of Science 69: 452–473
Other Internet Resources
- Evolution 101: How It Works, at the Understanding Evolution website, maintained at the University of California/Berkeley.
- Natural Selection: How Evolution Works, at ActionBioscience.org, maintained by the American Institute of Biological Science.
Related Entries
adaptation and adaptationism | biology: philosophy of | causation: probabilistic | character/trait | creationism | Darwinism | fitness | genetics: and genomics | genetics: evolutionary | genetics: genotype/phenotype distinction | genetics: population | heritability | laws of nature | life | natural selection | natural selection: units and levels of | probability, interpretations of | scientific explanation | species | teleology: teleological notions in biology

